独立懸架のロール| ロールとロールセンターの真実:基礎編 ③
[クルマの運動学講座・その12]
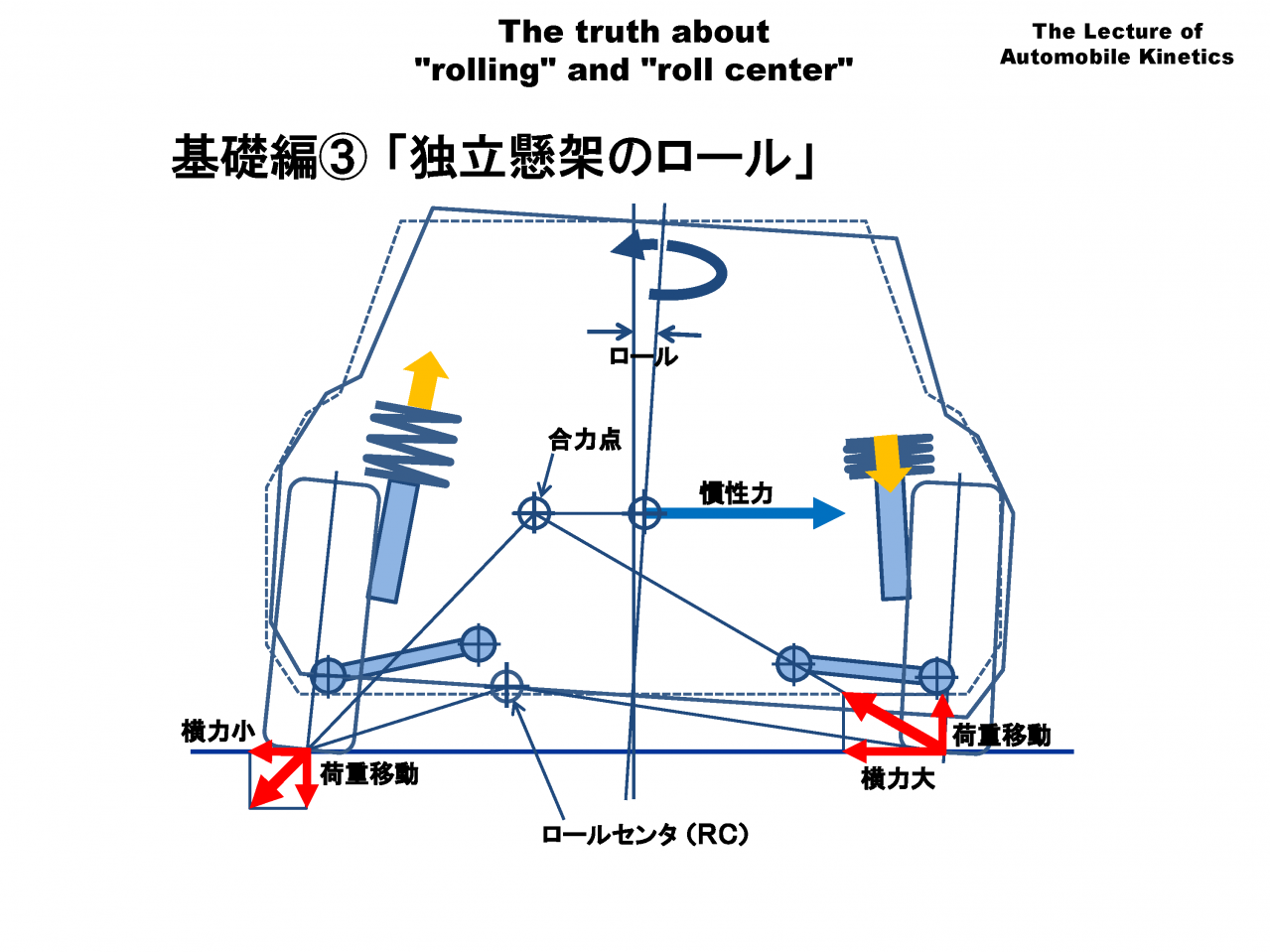
それでは、いよいよ基礎編③「独立懸架サスペンションのロール」の講義を始めます。
今回題材とするのは、ストラット式サスペンションです。ダブルウィッシュボーン式でもマルチリンク式でも考え方は同じです。
「ロールセンターの作図法」とか、いちいち覚える必要はないのでご安心ください。おしなべて学習で必要なのは「暗記」ではなく「理解」です。
TEXT&FIGURE:J.J.Kinetickler
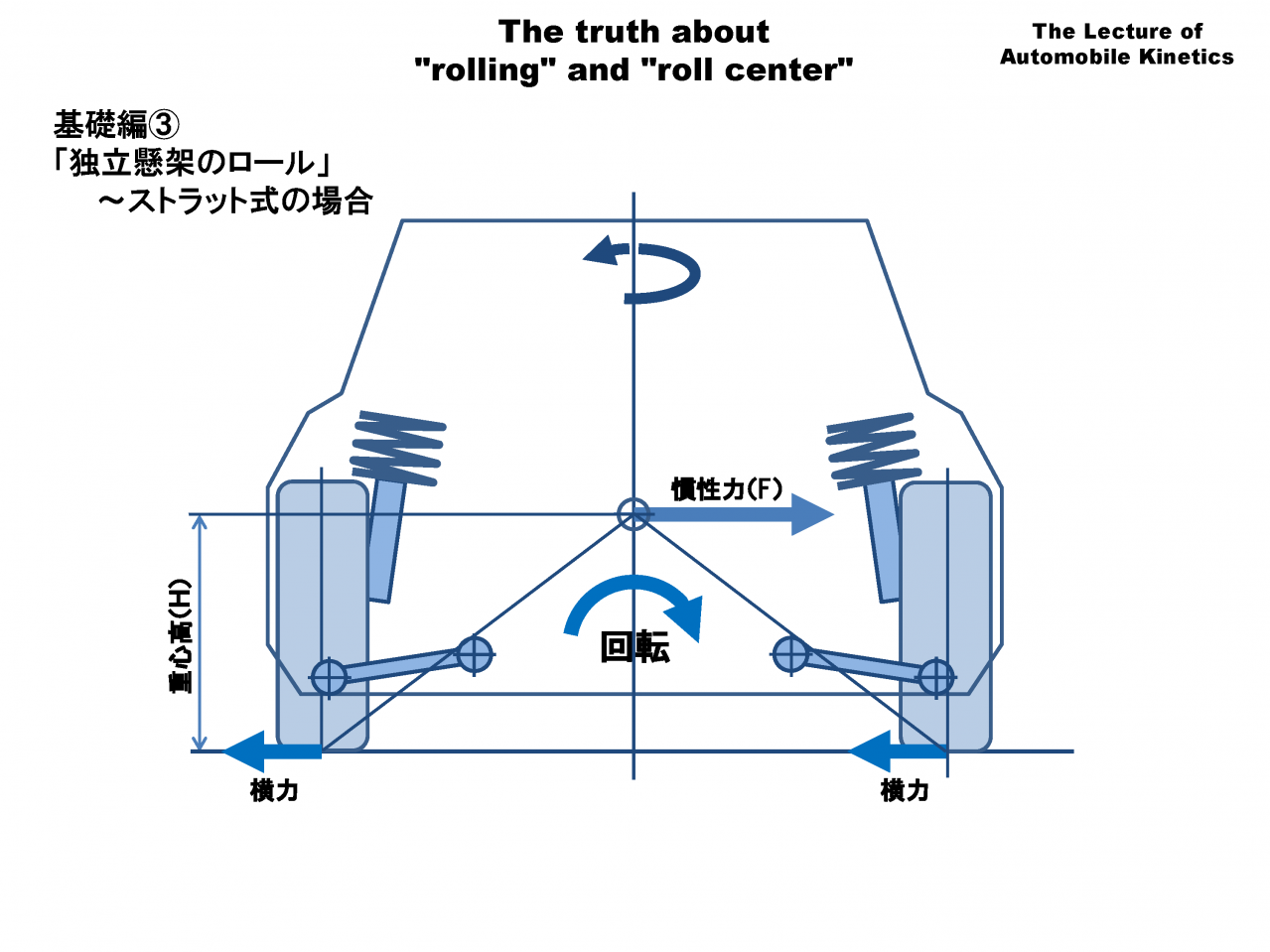
今までのおさらいです。
これは、独立懸架のクルマの旋回時の力の釣り合いです。横力と荷重移動と慣性力(遠心力)の釣り合いはリジッドアクスルの場合と同じです。横力は左右輪が均等に負担すると仮定しています。
旋回を始めると接地点に横力が発生し、その反作用として重心に慣性力(遠心力)が生じます。
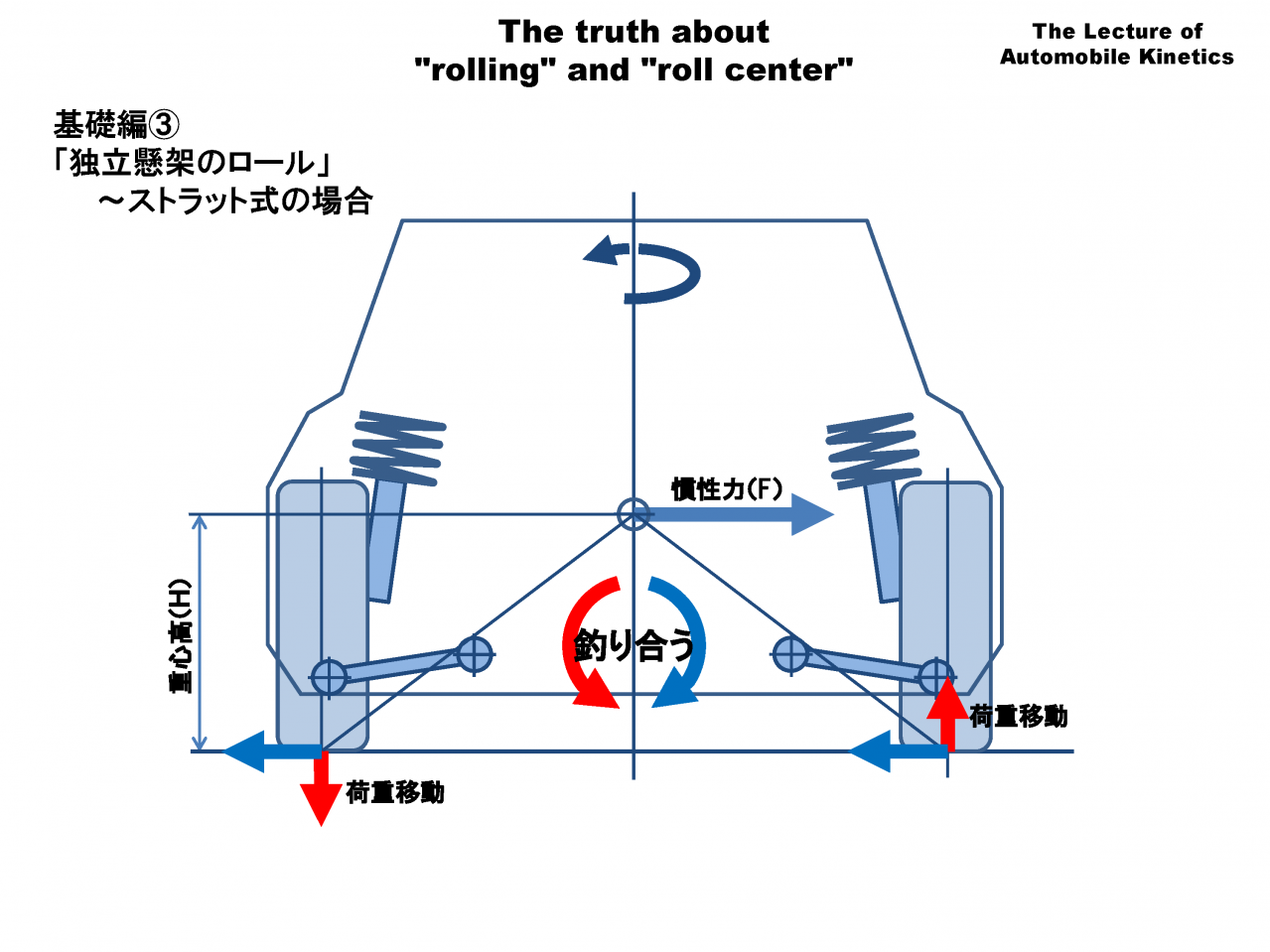
慣性力と横力は重心の高さ分だけ上下にずれているので、荷重移動がおこります。これもリジッドアクスルの場合と同じですね。
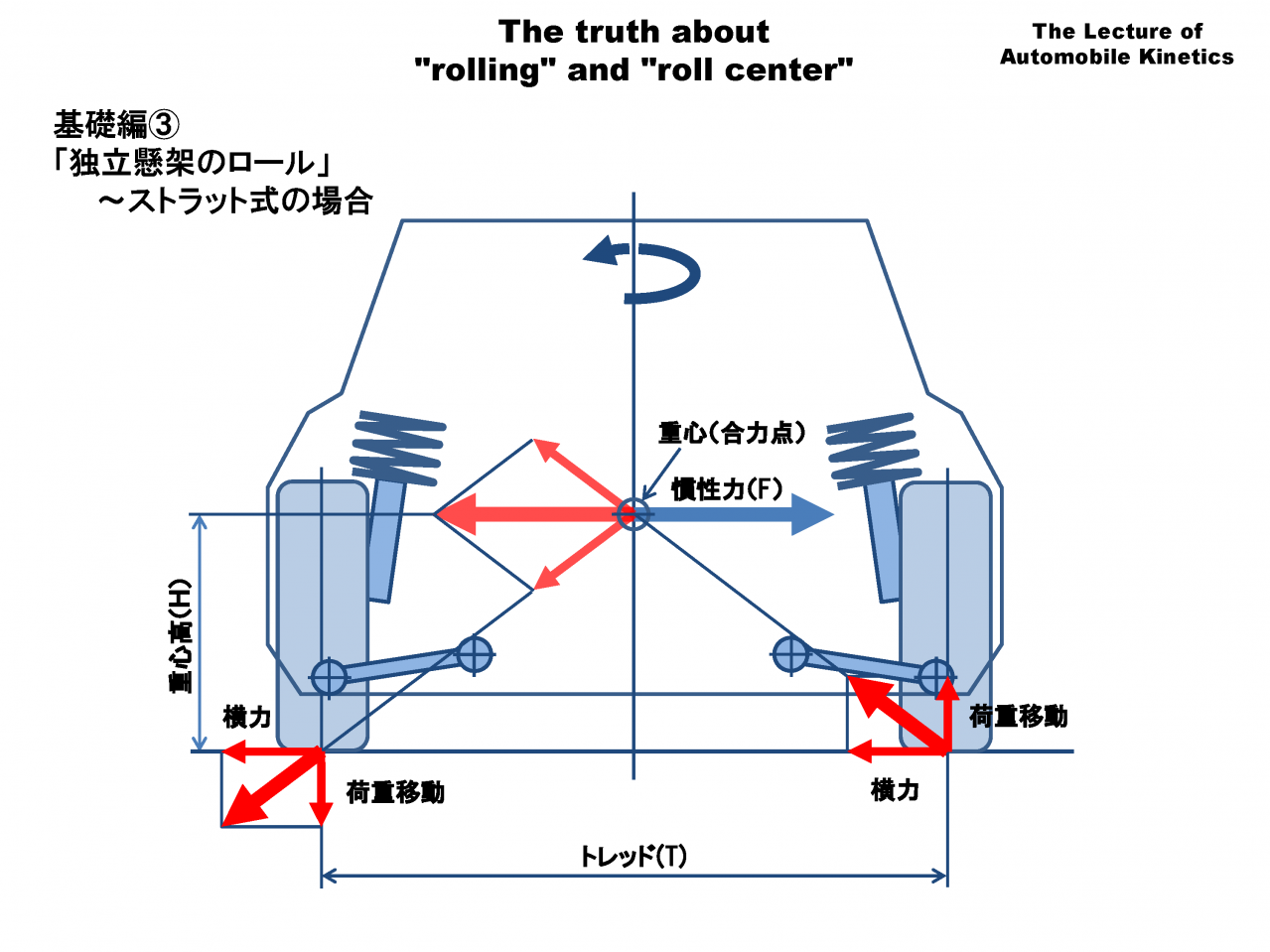
慣性力、横力、荷重移動は重心の高さで釣り合います。左右輪の横力が等しいと仮定しているので、全ての力が釣り合う「合力点」は重心と一致します。
タイヤ接地点での力の釣り合いはサスペンションとは無関係で、慣性力と重心高、トレッドだけで決まります。
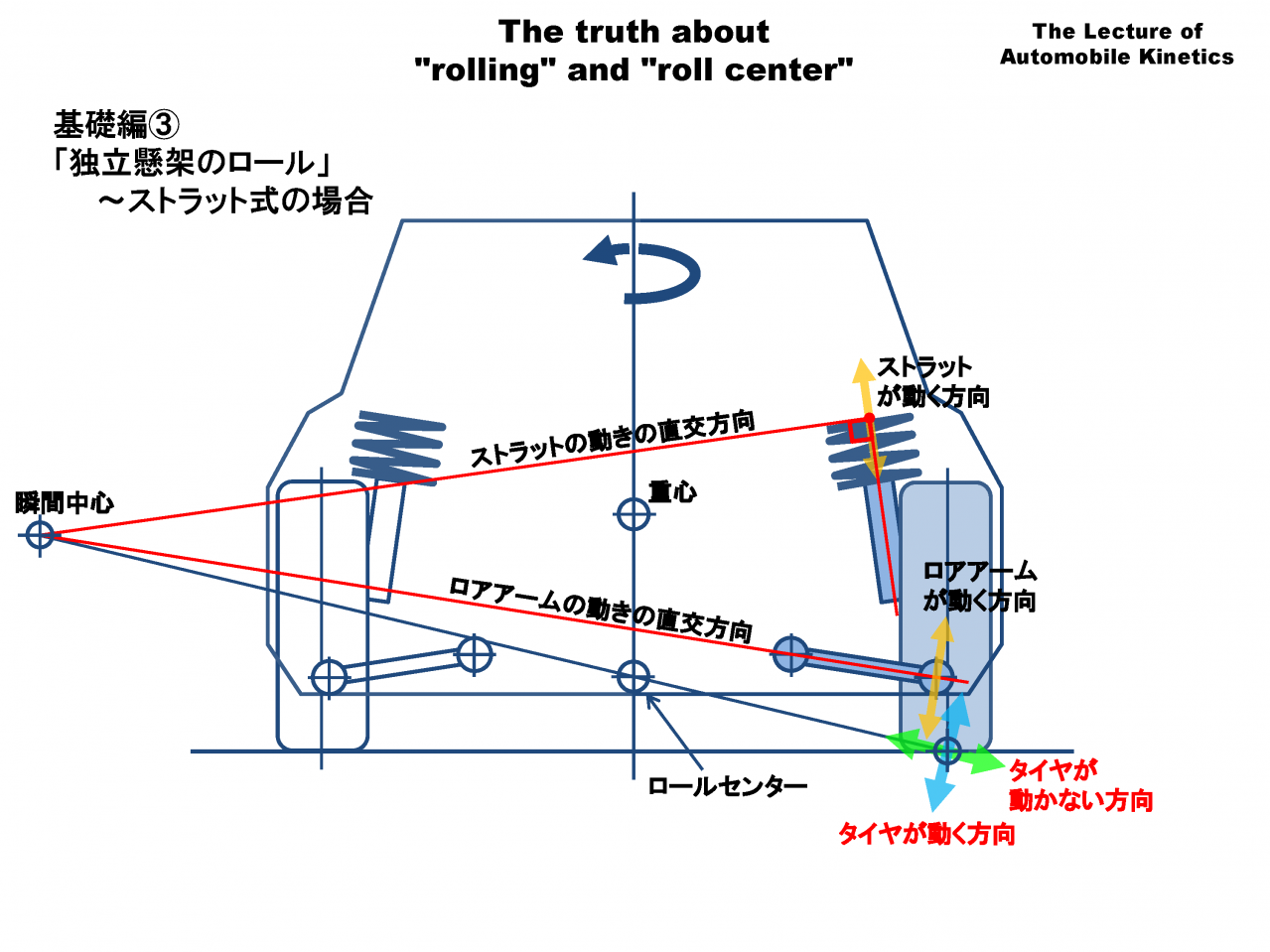
それでは、サスペンションに力が加わった場合の力の釣り合いを考えましょう。独立懸架では左右のサスペンションが繋がっていないので左右を別々に考える必要があります。
この図は教科書やネットにも書かれている「ストラット式サスペンションの瞬間中心とロールセンターの求めかた」です。
「瞬間中心」というのは、ひとカタマリの部品(この場合はタイヤとストラット)がある瞬間に2カ所以上共通して持っていると「いえる」中心のことです。
「いえる」というのが実は微妙で、このストラット式サスペンションの場合だと、ロアアームの実際の回転中心は車体側取付部、ストラットはストラットに直交する線の無限遠方にあるので共通の中心はありません。
しかし、ほんのわずかのサスペンションストロークの間なら、ここにあるといってもおかしくないといえる点が「瞬間中心」です。
しかし、この作図は不正確、あるいは無意味です。実際にはサスペンションアームが3次元的に傾いていたり、また上下のストロークで瞬間中心が大きく動くので、作図では簡単には決められないからです。
本当に正しく意味があるのは、赤字で書いたタイヤの接地点が動く方向と動かない方向だけです。これがわかれば、どんなサスペンションでも瞬間中心の方向とロールセンターを正確に求めることができます。
逆にいうと、この接地点の動く方向(軌跡)を簡易的に求める方法がロールセンターの作図です。
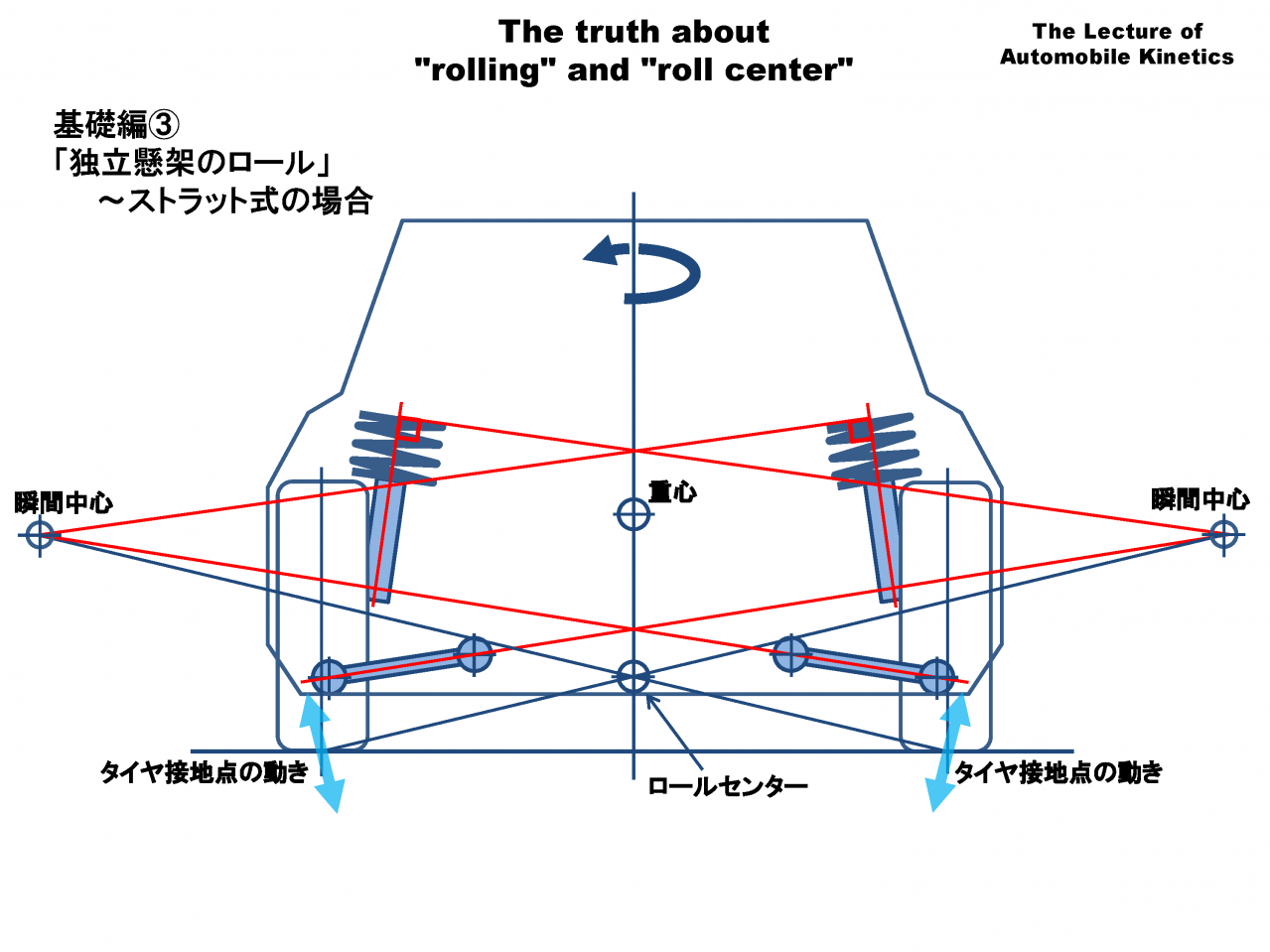
それでは、ストラット式独立懸架のロールとロールセンターについて考えましょう。
先にも述べましたが、この図のような「ロールセンターの作図法」をサスペンション形式毎に、いちいち覚える必要はありません。
実際に知る必要があるのは水色の両矢印で描いた「タイヤ接地点の動き」です。独立懸架の場合、瞬間中心はストロークによって大きく揺れ動くので、タイヤ接地点の動きは大抵の場合、直線でも円弧でもなく複雑な曲線です。
必要なのは旋回内外輪のタイヤ接地点の動き(水色の両矢印)と、それに直交する線(法線)の方向です。
実車でも車高を変えながらトレッドを測定することでタイヤ接地点の動きから実測でロールセンターを求めることができます。
左右のタイヤ接地点の動き(軌跡)の法線(直交した線)の交点をロールセンターと呼びますが、このロールセンターに大した意味はありません。
意味があるのはタイヤ接地点の動きだけです。この動きの直角(法線)方向のどこかに瞬間中心があるのですが、それがどこにあるのかも考える必要はありません。必要なのはその方向です。
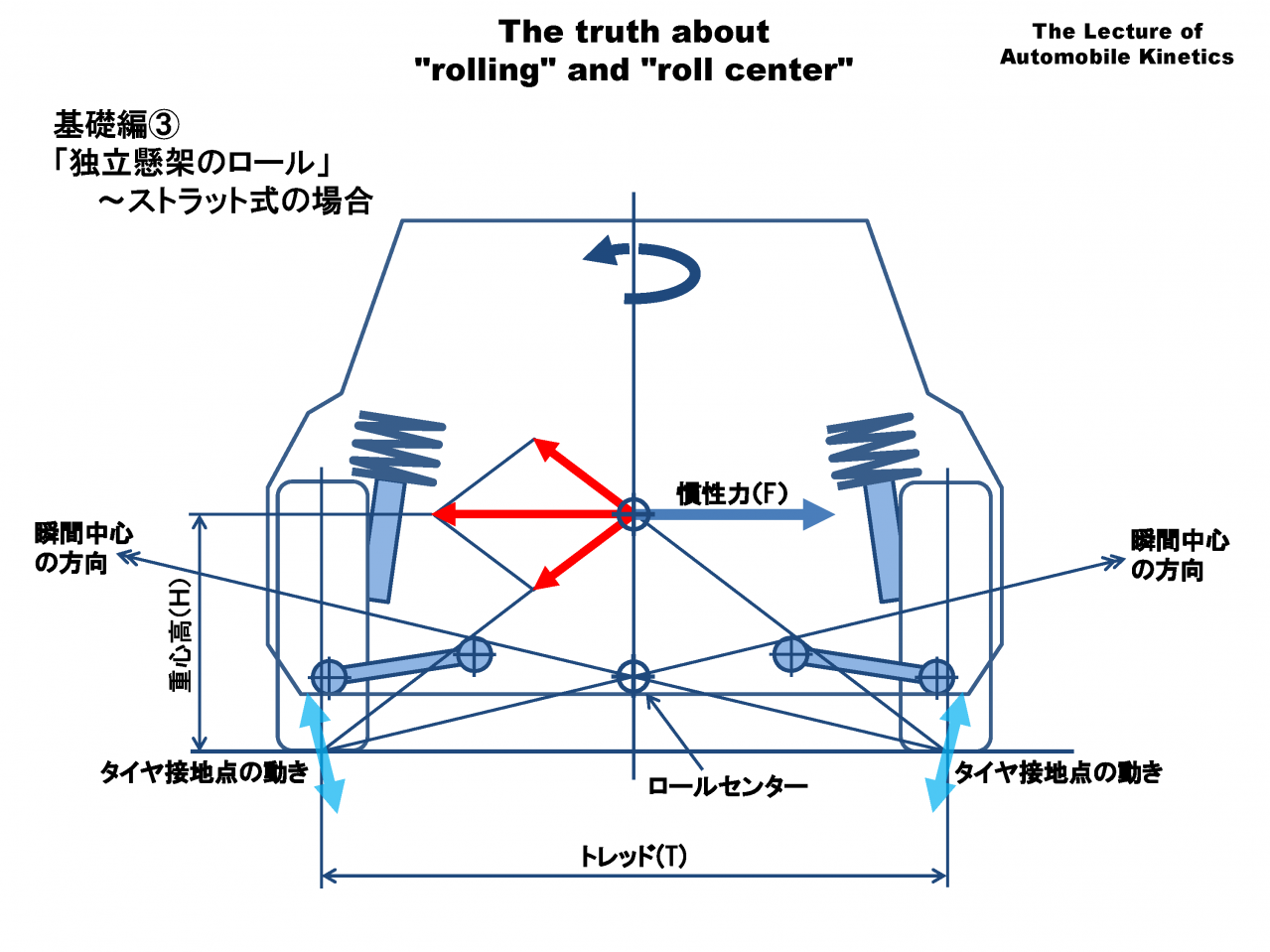
これは、独立懸架のクルマの旋回時の力の釣り合いです。とりあえず横力は左右輪が均等に負担すると仮定します。
タイヤ接地点での力の釣り合いはサスペンションとは無関係で、慣性力と重心高、トレッドだけで単純に決まります。
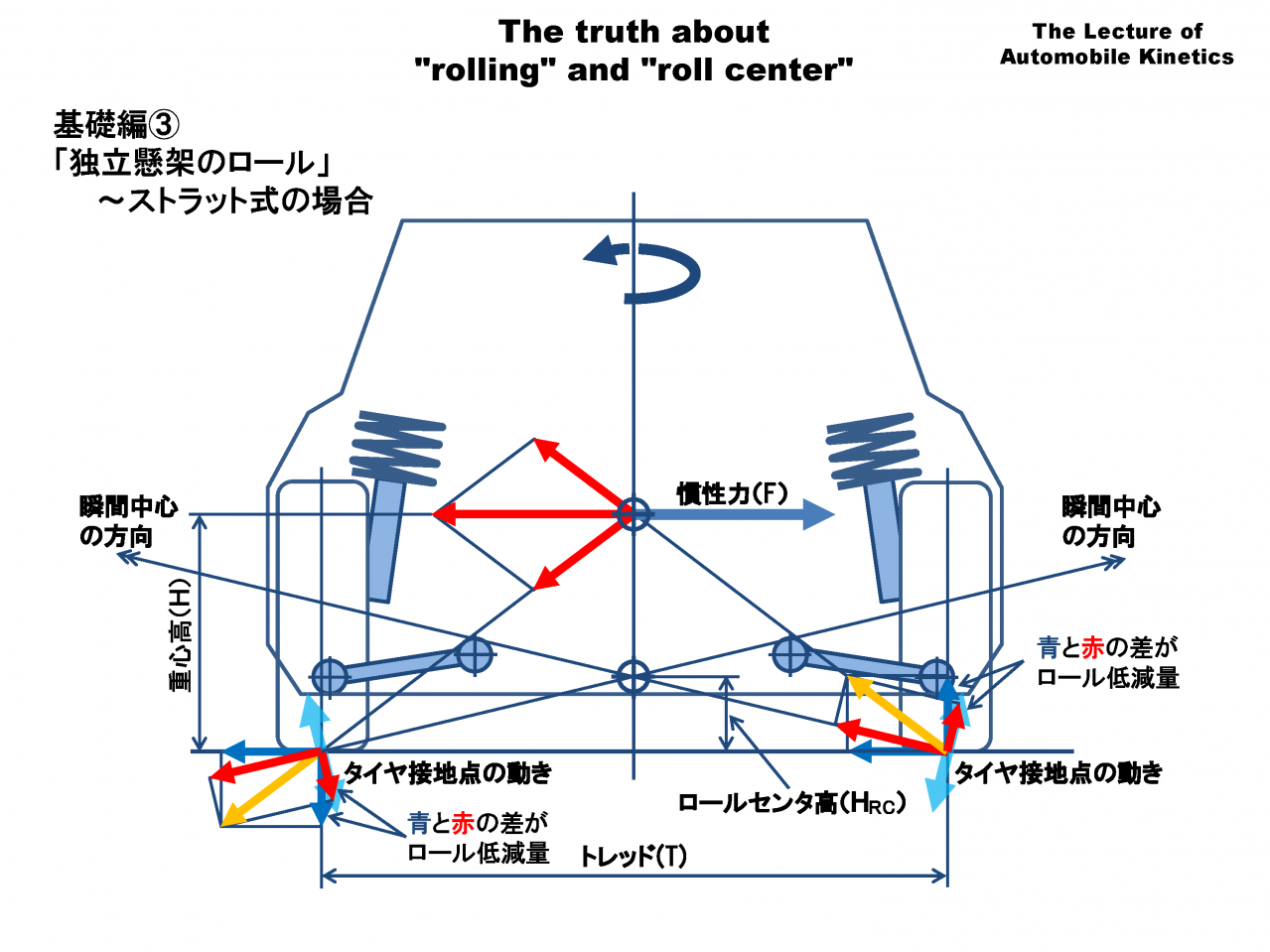
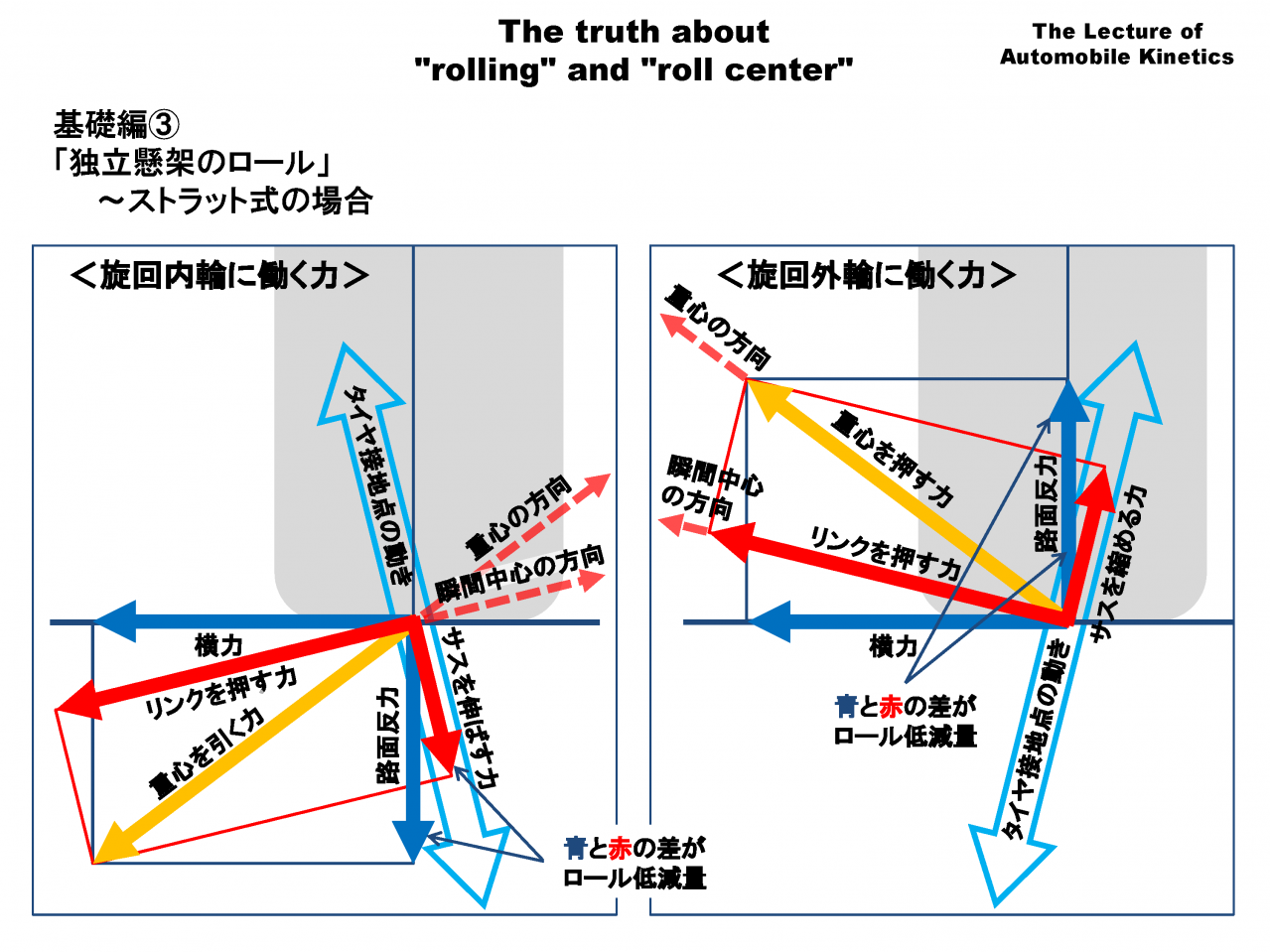
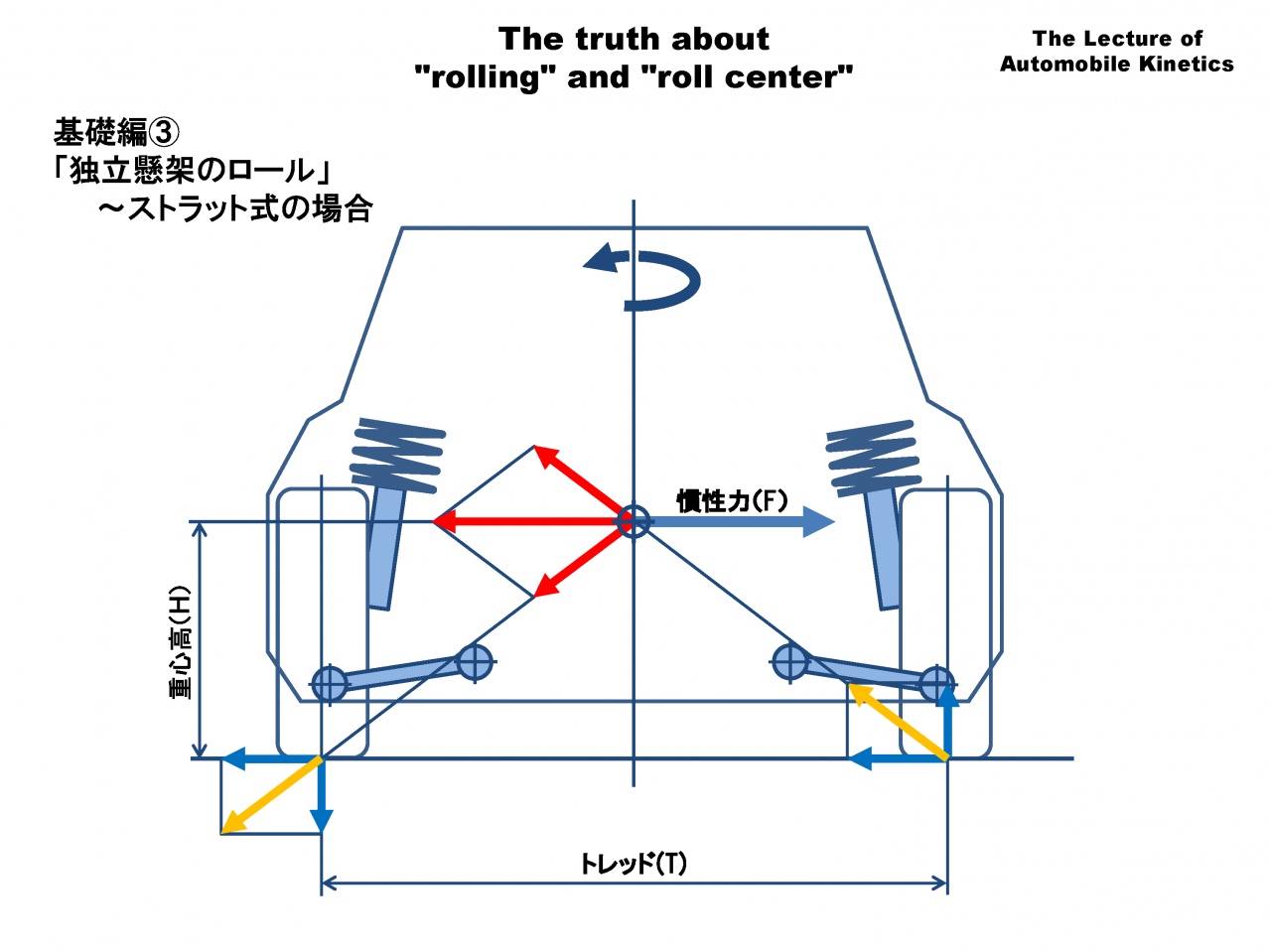
先程の図に、タイヤ接地点の動きを重ね描きします。瞬間中心の方向がサスペンションが力を受け止める方向で、その直角のタイヤ接地点の動きがスプリングに力を伝える方向です。
旋回内外輪の横力+荷重移動のベクトル(橙色)をタイヤ接地点の動きと瞬間中心に向う方向に分解(赤色矢印)します。
青矢印の「横力、荷重移動」を赤矢印の「瞬間中心に向かう方向、タイヤ接地点の動きの方向」に分けて考えるとロールセンターやアンチロールのメカニズムを理解することができます。
図が見にくいので、次の図で内外輪の接地点を拡大してみましょう。