前軸と後軸の荷重移動| ロールとロールセンターの真実:基礎編 ⑤
[クルマの運動学講座・その14]
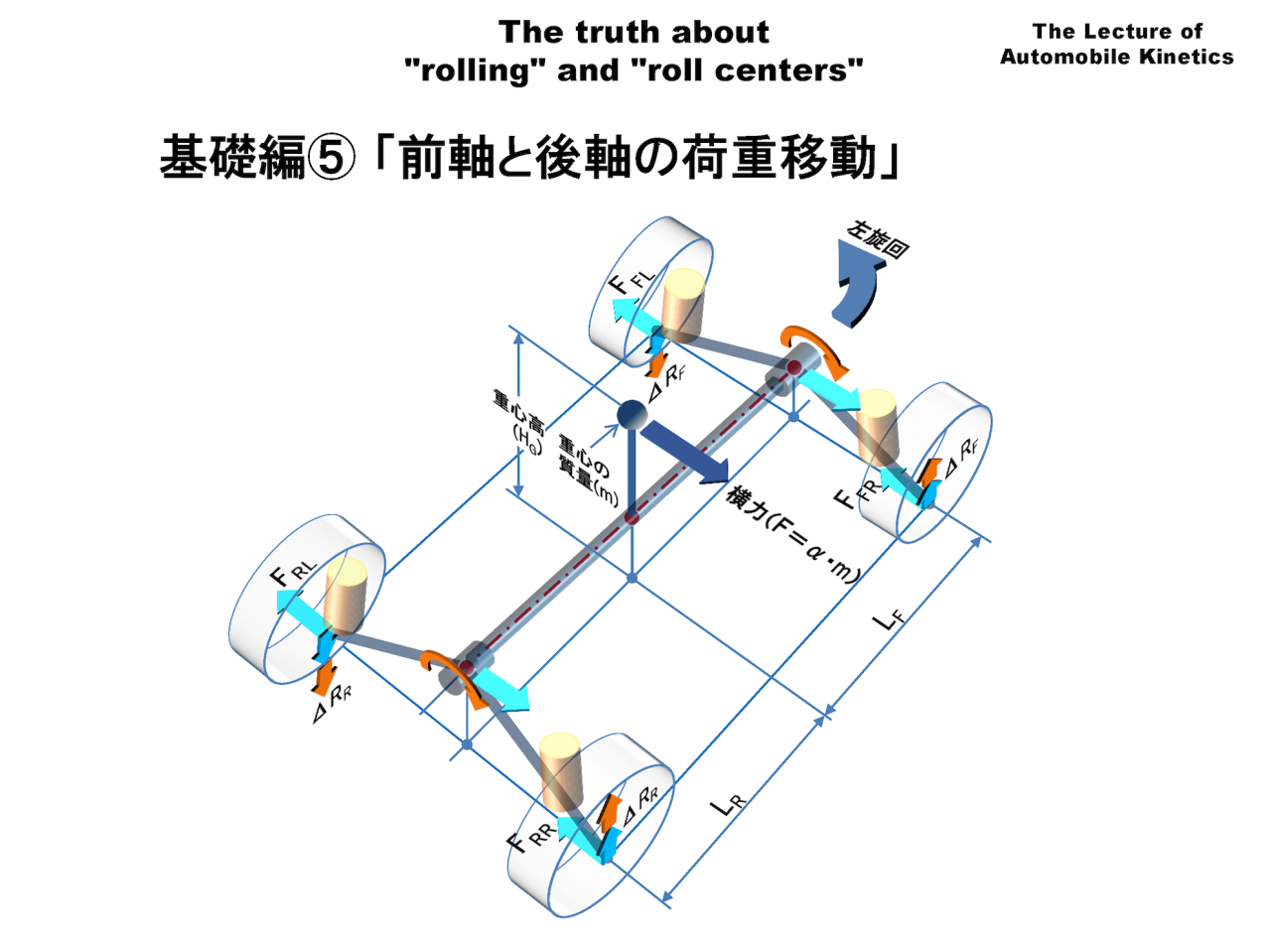
これまではロールやロールセンターについてクルマを背面からみた図を使って、2次元的に講義してきましたが、今回は前後サスペンションを関連付けて、クルマ全体を立体的に考えます。
少し難しく感じるかも知れませんが、順を追って理解していけば意外に容易です。
TEXT&FIGURE:J.J.Kinetickler
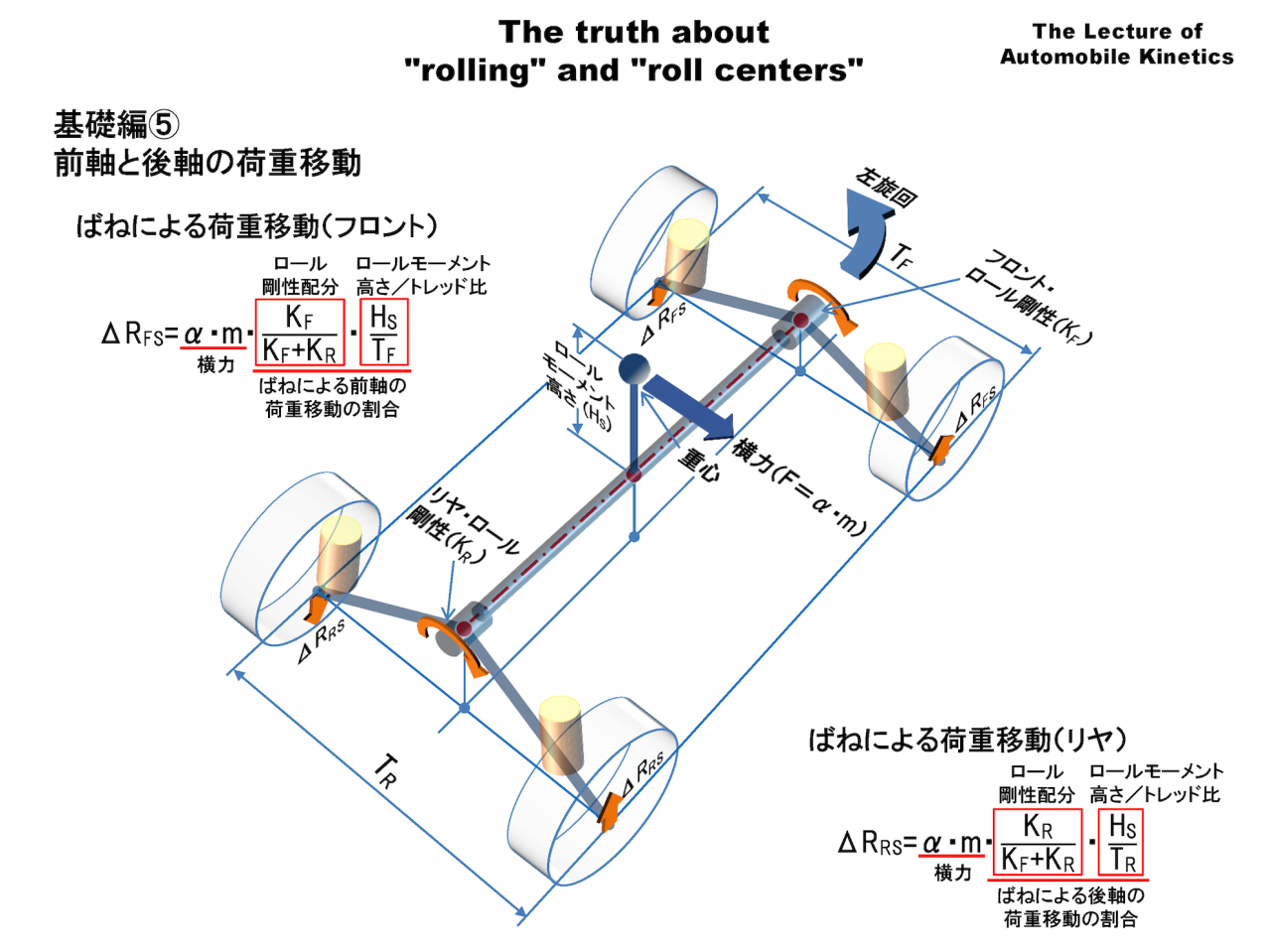
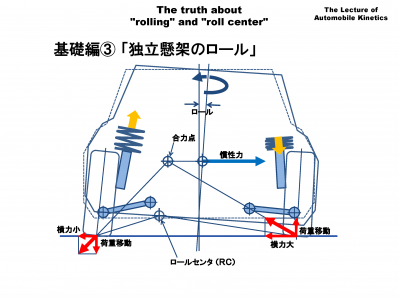
荷重移動を「ばねによる荷重移動」と「リンクによる荷重移動」に分けて考えます。 まず最初に、「ばねによる荷重移動」について解説します。
ばねによる荷重移動は通常、左右のコイルばねの伸縮により発生しますが、この簡易モデルはそれを「ロール剛性(KF、KR)」という考え方で表します。これにはコイルばねの他、スタビライザーのばねも含まれます。
「ばねによる荷重移動」は横力を伝えません。横力を伝えることができるのは、後で説明する「リンクによる荷重移動」だけです。これはぜひ覚えておいてください。
ロール剛性の単位はNm/radです。これは1rad(ラジアン:約57.3度)をねじるのに必要なねじりトルク(力×長さ)を表しています。
ばねによるクルマの荷重移動は図のロールモーメント高さ(HS)にあるばね上の重心に旋回時の横力F=α・mが加わることによって生じます。F(N)は力の単位でクルマのばね上質量m(kg)と横加速度α(m/s2)を掛けたものです。
前後のばねに加わるロールモーメント(MR)は以下の式で表せます。
ロールモーメント(MR) =α・m・HS(Nm)
一方、前後のコイルばねやスタビライザーによるロール剛性は次のように前後に分配されます。
ロール剛性のフロント配分 =KF/(KF+KR)
ロール剛性のリヤ配分 =KR/(KF+KR)
ロールモーメント(MR)にロール剛性の前後の配分を掛けてトレッド(T)で割ったものが「ばねによる荷重移動(ΔRFS、ΔRRS)」です。
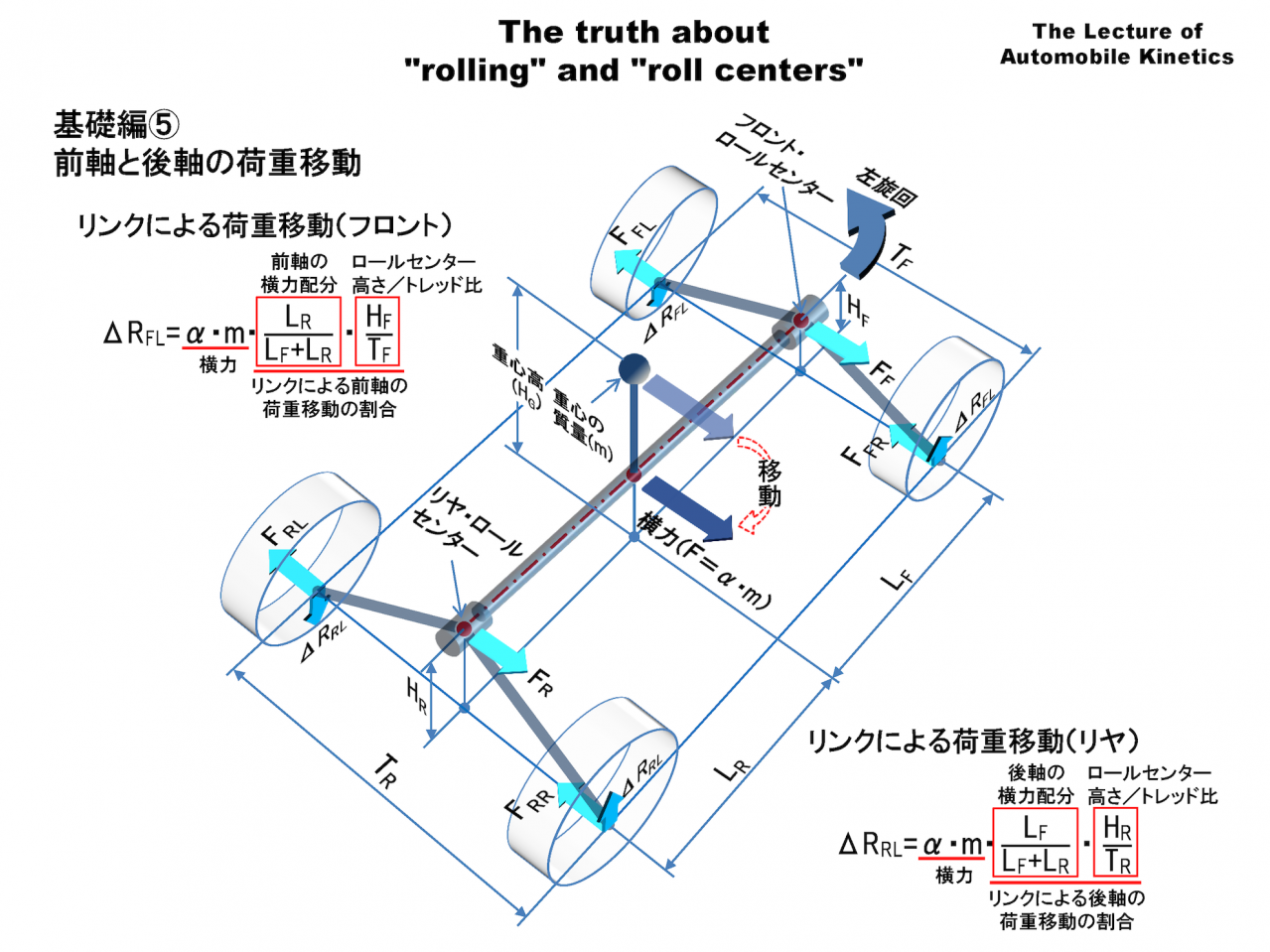
次に「リンクによる荷重移動」について解説します。 リンクによる荷重移動は次にように考えます。
「ばねによる荷重移動」では横力は伝えられないのでロールモーメント(MR)として加えましたが、残った横力は重心の真下のロール軸のところまで移動させ、ロール軸に直接加えます。
重心の真下のロール軸に加わった横力が「てこの原理」で前後のロールセンターに配分されます。その配分の割合は以下のようになります。 たとえば重心がフロント寄りならフロントに多く配分されます。
横力のフロント配分 FF=LR/(LF+LR)
横力のリヤ配分 FR=LF/(LF+LR)
リンクによる前後サスペンションの荷重移動は旋回時の横力(F)に横力の前後配分を掛けた力が前後のロールセンターに加わることによって生じます。
横力の前後配分にロールセンター高を掛け、トレッドで割ったものが「リンクによる荷重移動(ΔRFL、ΔRRL)」です。
リンクによる荷重移動(フロント) ΔRFL =FF× HF/TF
リンクによる荷重移動(リヤ) ΔRRL=FR× HR/TR
リンクによる荷重移動は重心の前後位置と前後のロールセンターの高さにより自由に変えることができます。たとえば前輪のロールセンターが路面にあれば前輪のリンクによる荷重移動はゼロになります。しかしこの場合でも横力だけは伝えられます。
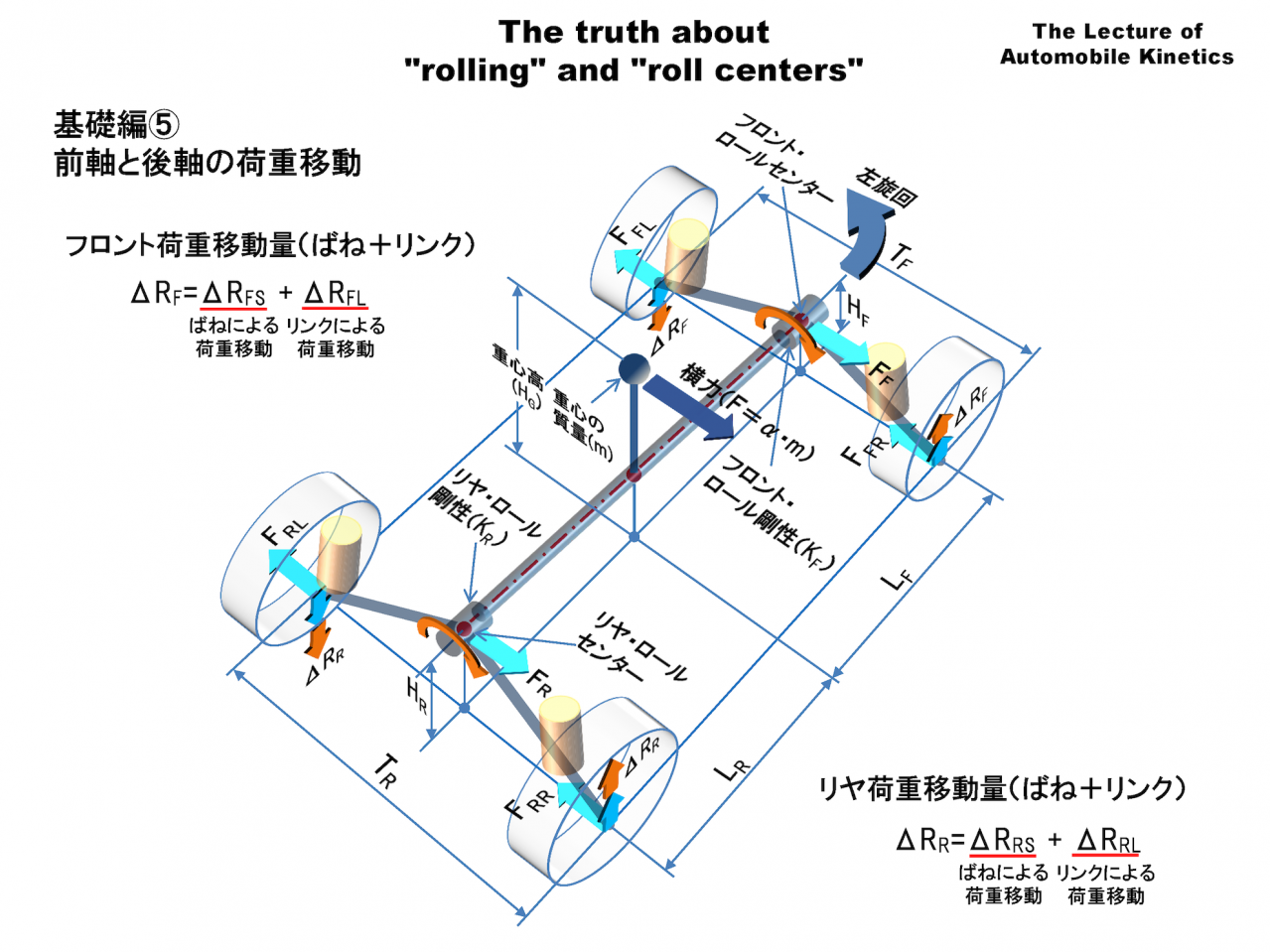
そして、ばねによる荷重移動とリンクによる荷重移動を足し合わせたものが全体の荷重移動です。
フロントの荷重移動 ΔRF=ΔRFS+ΔRFL
リヤの荷重移動 ΔRR=ΔRRS+ΔRRL
前後の荷重移動は、ばねとリンクの設定でどのようにも設定できます。しかし前後の荷重移動を合計した全体の荷重移動は変わりません。荷重移動を減らすには重心高を下げるかトレッドを広げるしかありません。
これを眺めていると例えば、リヤが全く荷重移動しないサスペンションや逆に荷重移動するサスペンションもできることがわかります。
リヤのロール剛性をゼロ、ロールセンターを路面にするとフロントで100%荷重移動を受け止めることになります。
この状態からさらにリヤのロールセンターを路面より低くすると荷重移動がマイナスになります。旋回外輪から内輪に荷重移動するわけです。
しかしトータルの荷重移動は重心高とトレッドだけで決まるので、この場合はフロントが100%以上の荷重移動を受け持つことになり、たとえばフロントが120%、リヤがー20%、トータル100%のようなことになってしまいます。
これを実現する具体的なサスペンションは後でお見せします。