『トラクション』 ってなんだ？ 『パワー』ってなんだ？ ｜ ①大パワーのFFがない理由（トラクション効率）

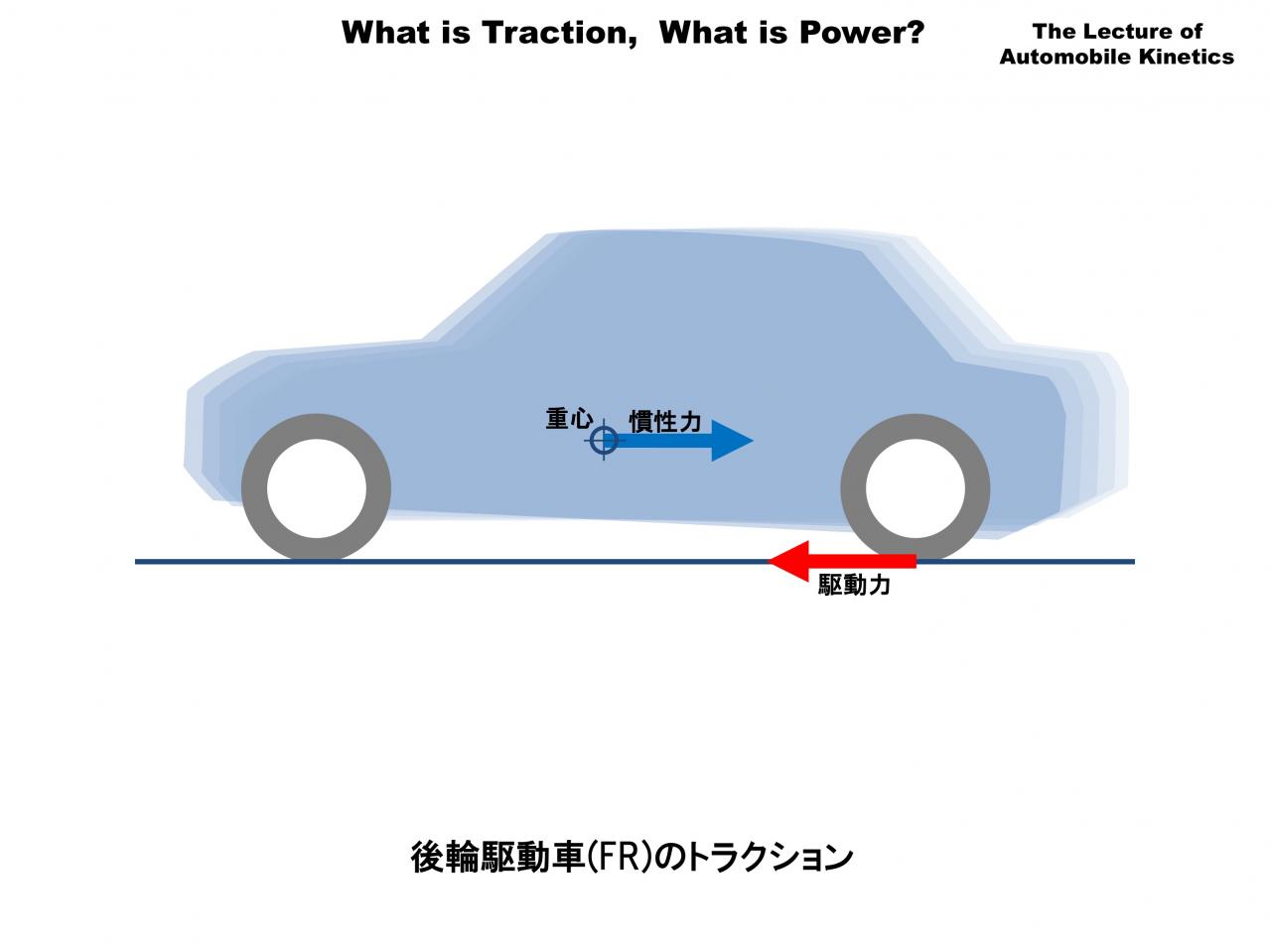
これはFR車が加速している時のイメージです。後輪が駆動力を路面に伝え、その反力（反作用）でクルマが加速する。「えっ？矢印の向きが両方とも逆じゃないの？」…といきなり思ったあなたは鋭いです。

わかってみれば簡単なことなのですが、これはクルマが受ける力のやり取りで考えているためです。「クルマが地面に蹴られ、加速させられる力」を「駆動力」、それに抵抗して「クルマをそこに留まらせようとする力」を「慣性力」と名づけています。この表現に段々と慣れていただければと思います。

駆動力は路面とタイヤの摩擦力で伝わるのですが、その大きさの限界は接地荷重および路面とタイヤの摩擦係数によって決まります。

接地荷重はそのクルマの重心に働く重力によるものと、加速時の動的な荷重移動を足し合わせたものになります。

動的な荷重移動は加速度に比例するだけではなく、時間と共に刻々変化するのですが、これはやや難解なので別の機会に譲りたいと思います。ここでは一定の加速度で力が釣り合っている状態を解説します。

動的な荷重移動と路面とタイヤの摩擦力によって伝えることができる駆動力を「トラクション」と呼びます。クルマのエンジンやモーターが発生する駆動力より「トラクション」が小さいとタイヤがホイールスピンを始め、加速が制限されてしまいます。

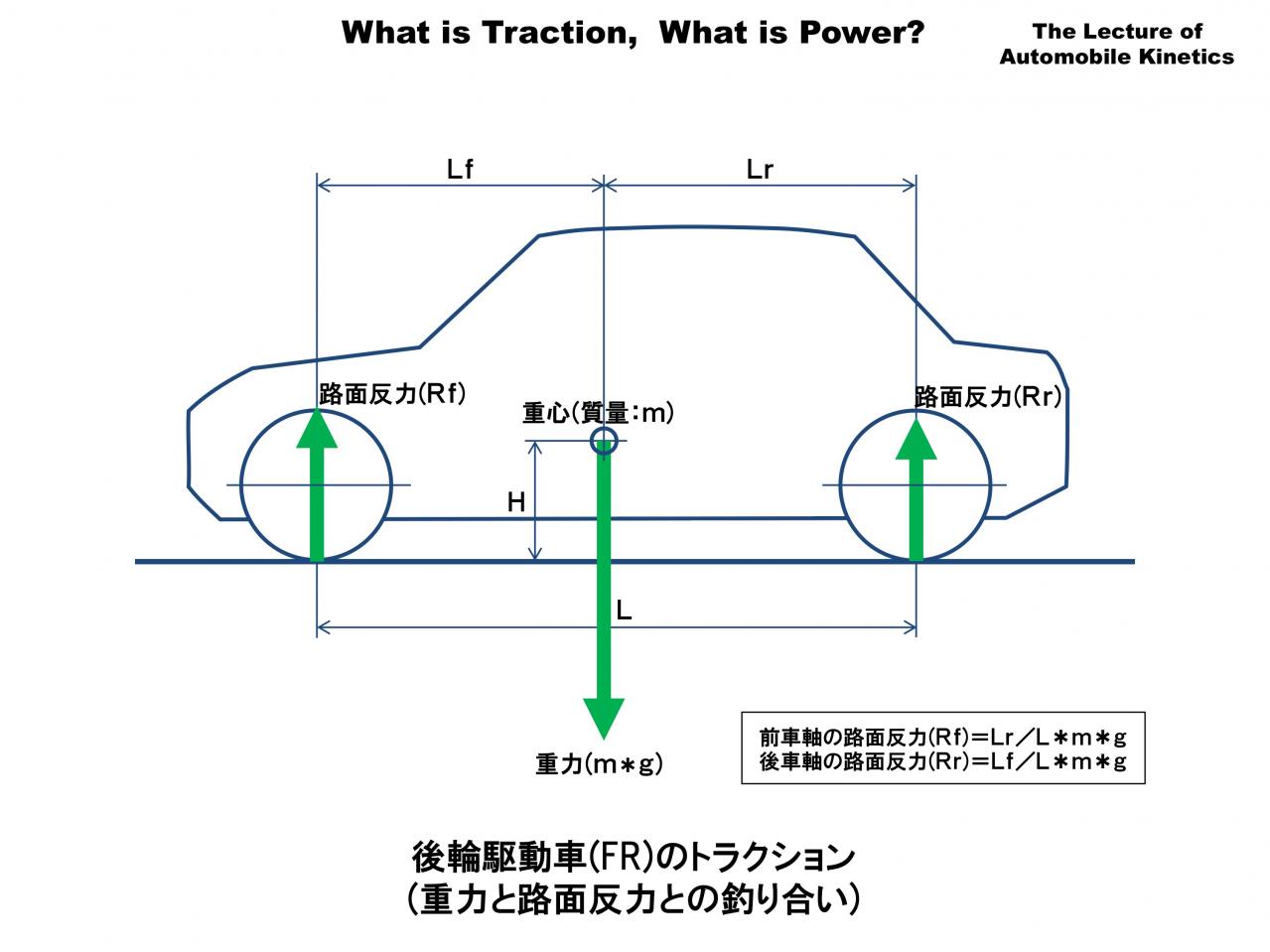
この図は静止している状態のFR車です。重心に重力が加わっています。重力はクルマと地球が引っ張り合う力なので下向きです。それと釣り合う力が路面反力です。重力と釣り合う力なので路面反力は上向きの力です。

「クルマが地面を押しているのだから下向きでは？」と考えてしまいますが、クルマ基準で考えると「クルマが地面から押し返される力」なのでやはり上向きです。

「力はどこかで釣り合っている」と考えましょう。この場合は重力と路面反力が上下で釣り合っています。

前後それぞれの路面反力はホイールベースのどこに重心があるのかで決まります。
　前車軸の路面反力(Rf)=前輪荷重配分(Lr/L)×質量(m)×重力加速度(g)
　後車軸の路面反力(Rr)=後輪荷重配分(Lf/L)×質量(m)×重力加速度(g)　になります。

Rfの式にはLrを使い、Rrの式にはLfを使うことに、ちょっと注意してください。この釣り合いは天秤と同じなので重心が前にあるほど前車軸の路面反力が大きくなるということで理解できますね。

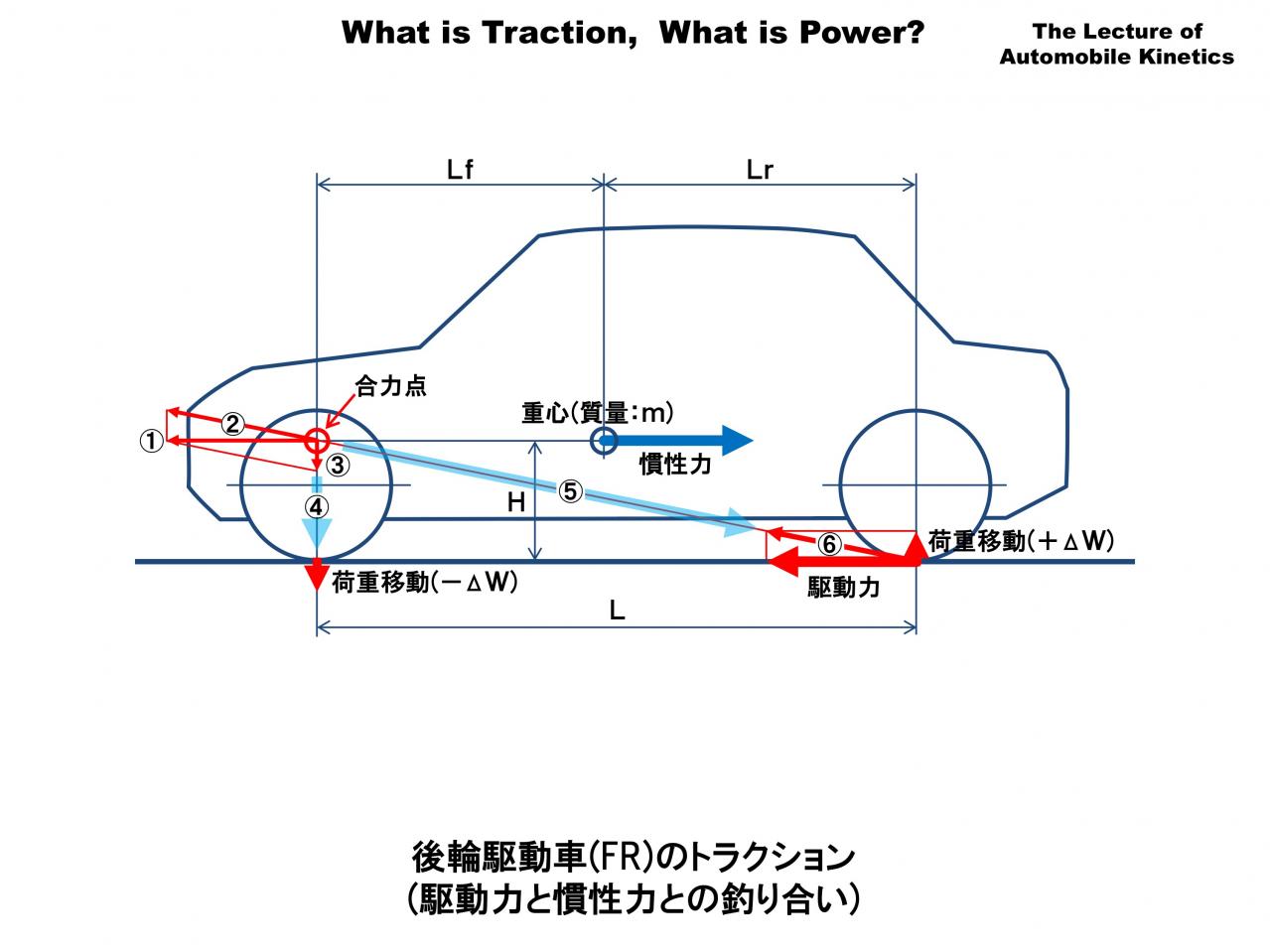
次はいったん、重力のことは忘れていただいて、駆動力と慣性力の釣り合いだけを考えます。「力はどこかで釣り合っている」といいましたが、冒頭の図では釣り合うはずの駆動力と慣性力が上下にずれています。

このままでは向きが逆で同じ大きさの力を加えても釣り合わず、車体がくるくる回ってしまいます。これを釣り合わせるためには別の力が必要です。それが荷重移動です。駆動力と慣性力に荷重移動を加えると全ての力が釣り合います。いいかえれば「釣り合うように荷重移動している」わけです。全ての力(この場合は駆動力、荷重移動、慣性力)が一点で釣り合う点を「合力点」と呼びます。

計算式では　荷重移動量(ΔW)=質量(m)×加速度(α)×重心高(H)÷ホイールベース(L)　になりますが、この図をみて理解した方がわかりやすい…というか今後のことも考えて作図して考えることに慣れましょう。

作図は簡単です。後輪駆動車の場合、合力点は重心の高さで前輪の真上にあります。この合力点から慣性力と同じ長さで向きが逆のベクトル(①)を描きます。このベクトルが慣性力と釣り合う力です。このベクトルを図のように後輪の接地点に向かう力(②)と前輪の接地点に向かう力(③)に分解します。ベクトルの分解は図のように平行四辺形を描いて作図します。

前輪の荷重移動ベクトル(③)は、そのまま前輪の接地点まで移動(④)します。後輪へ向かうベクトル(②)は一旦後輪の接地点まで移動(⑤)し、移動したベクトル(⑥)をさらに水平と垂直のベクトルに分解します。垂直方向が荷重移動、水平方向が駆動力です。

当然ですが作図でも駆動力は慣性力と向きが逆で大きさが等しく、前後荷重移動は計算の値と等しく、前輪の荷重移動は下向きで荷重が減少(-ΔW)、後輪は上向きで荷重が増加(+ΔW)になります。

ベクトルは普通の数字と同じように足したり、引いたり、分けたりできます。ベクトルと力の釣り合いの超簡単な説明が、ここ（ https://motor-fan.jp/tech/article/4062/ ）にあるのでご一読ください。

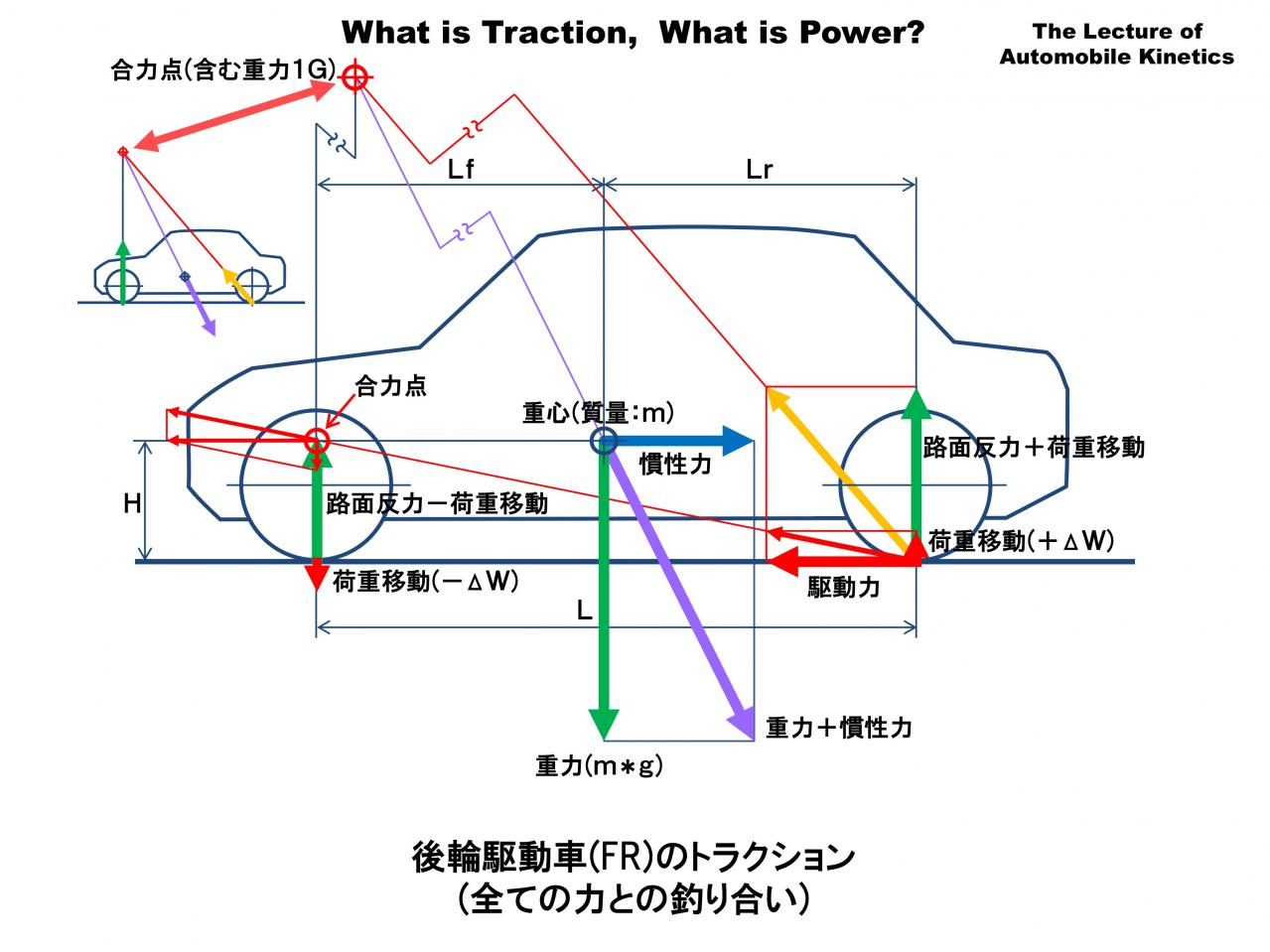
この図は先のふたつの図、重力の釣り合いと、駆動力の釣り合いを足し合わせたものです。重力と路面反力、駆動力と慣性力を足し合わせた力の合力点は前輪の真上でかなり高いところになります。このように力が釣り合っている時、どこかに合力点があります。

この合力点は駆動力が増減すると位置が上下します。重力は一定なので慣性力（＝駆動力）が増減すると重力＋慣性力をあらわす紫色の矢印の角度が変わるからです。

これはかなり面倒な作図なので、これからは駆動力と慣性力の釣り合いだけを考え、必要に応じて重力と路面反力の釣り合いを足し算することにしましょう。

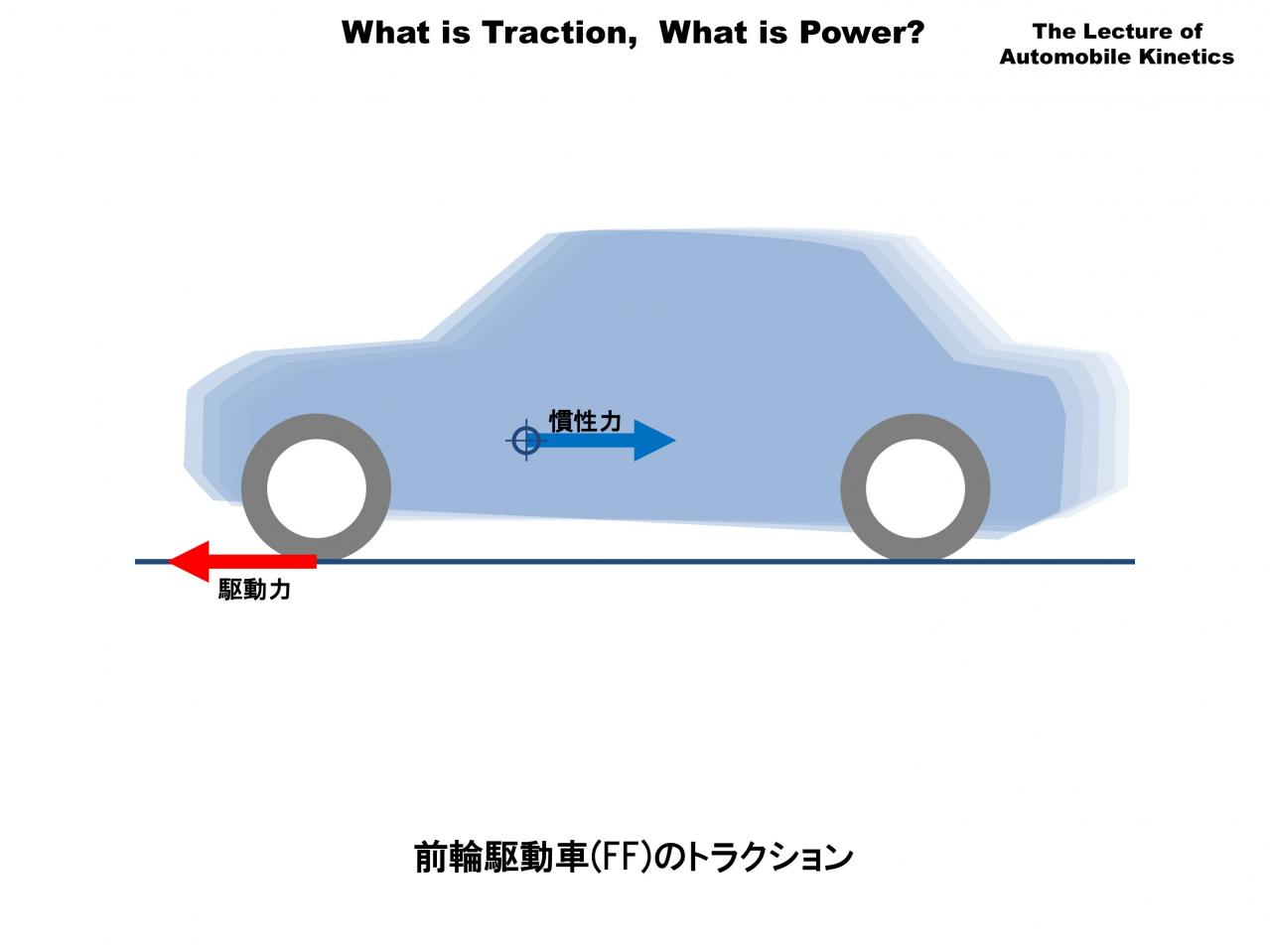
次は前輪駆動車（FF）の加速イメージです。前輪が駆動力を路面に伝え、その反力（反作用）でクルマが加速します。

FFでもFRでも同じですが「クルマが地面に蹴られ、加速させられる力」を「駆動力」、それに抵抗して「クルマをそこに留まらせようとする力」を「慣性力」と名づけています。後輪駆動車との違いは駆動力のベクトルが前輪にあることです。

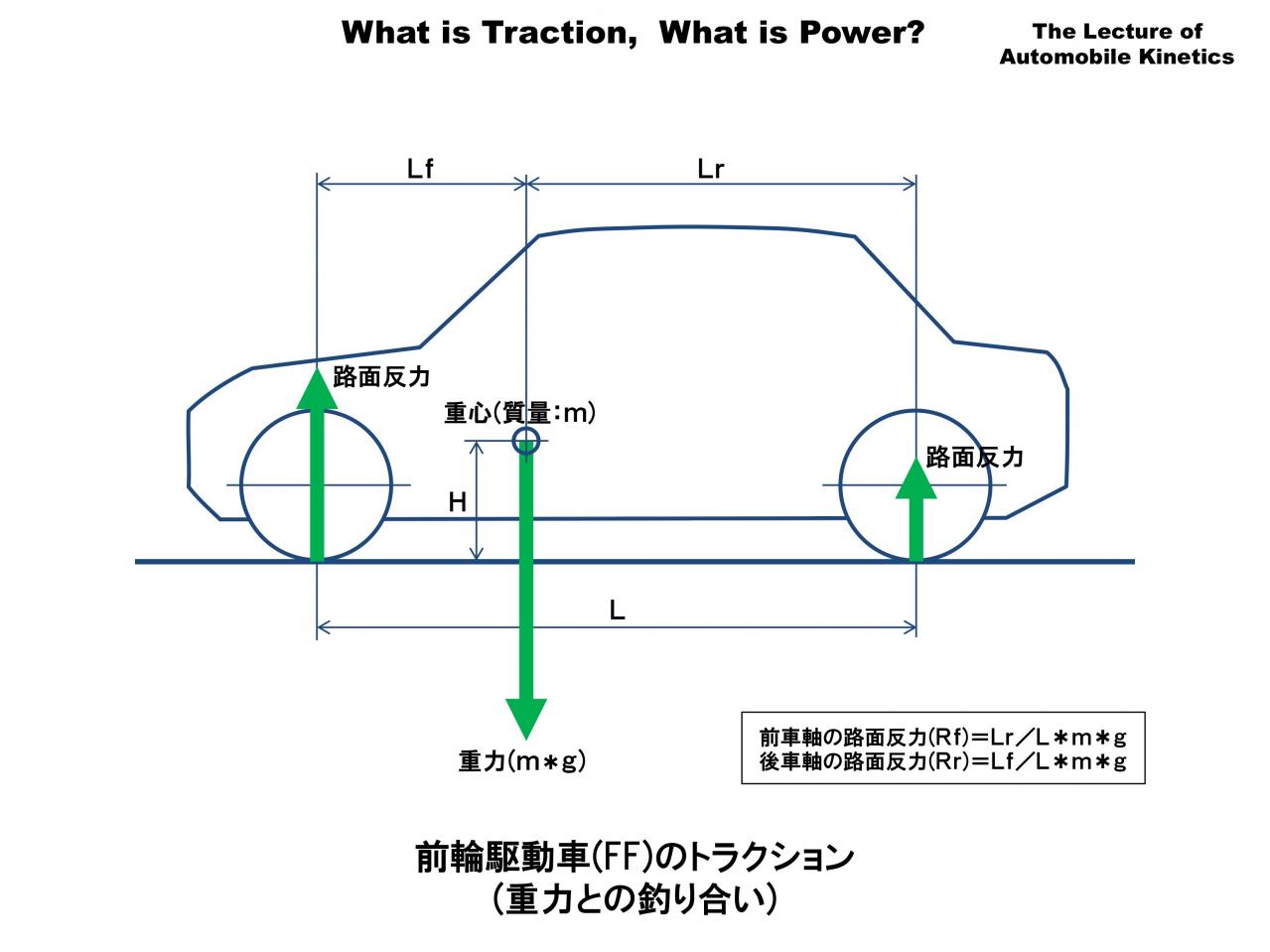
この図は静止している状態の前輪駆動車（FF）です。力の釣り合いの考え方はFRと同じですが、FFはパワートレインが前部に集中しているので重心位置が前方にあります。この図は前後輪の荷重配分を65:35で描いています。

前後それぞれの路面反力はホイールベースのどこに重心があるのかで決まります。
　前車軸の路面反力(Rf)=前輪荷重配分(Lr/L)×質量(m)×重力加速度(g)
　後車軸の路面反力(Rr)=後輪荷重配分(Lf/L)×質量(m)×重力加速度(g) 　になります。

FRと同じようにRfの式にはLrを使い、Rrの式にはLfを使うことにちょっと注意してください。

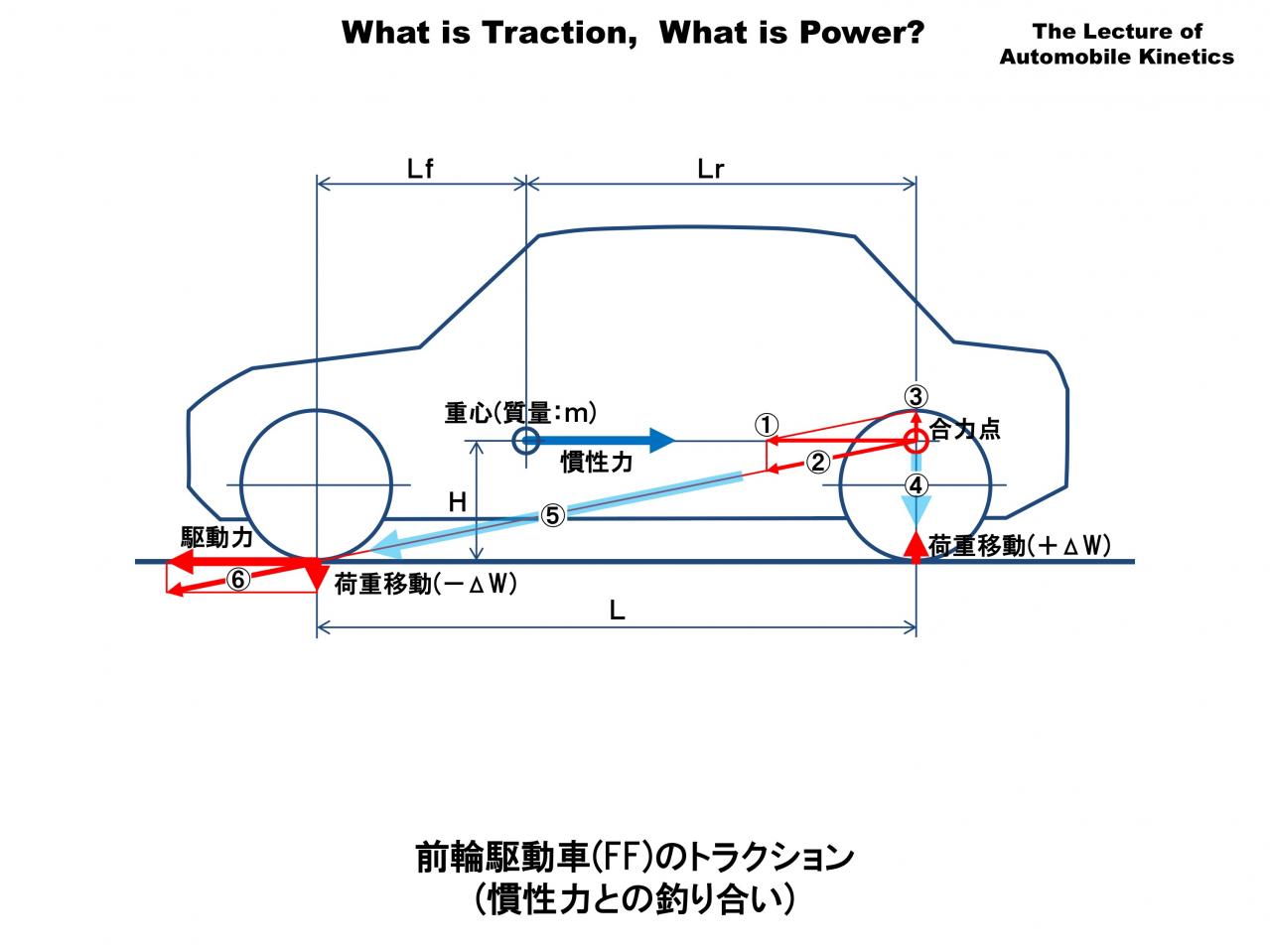
この図は前輪駆動車（FF）の駆動力と慣性力の釣り合いです。FRと同じように駆動力と慣性力が上下にずれているので、前後輪の間で荷重移動が発生します。

前輪駆動車（FF）の合力点（すべての力が釣り合う点）はFRとは逆の重心の高さで後輪の真上にあります。この点に慣性力と同じ長さで向きが逆のベクトル(①)を描きます。このベクトルを図のように前輪の接地点に向かう力(②)と後輪の接地点に向かう力(③)に分解します。ベクトルの分解は図のように平行四辺形を描いて行います。

後輪は分解したベクトルを接地点までそのまま移動(④)します。前輪は一旦前輪の接地点までベクトルを移動(⑤)し、この移動したベクトル(⑥)をさらに水平と垂直のベクトルに分解します。垂直方向が荷重移動で水平方向が駆動力です。当然ですが、駆動力は慣性力と等しく、前後荷重移動は計算の値と等しくなります。

この図で注目してほしいのは加速するとき駆動輪である前輪は荷重移動がマイナス（下向きのベクトル）になることです。加速すると接地荷重が減少するので前後荷重配分はあらかじめ前輪寄りになっている必要があります。

「クルマは50:50の前後バランスが理想」という方がおられますが、FFの場合はフロントヘビーでないとトラクションがかかりません。タイヤ容量が十分なら前輪荷重が65%くらいあった方が健全です。

一時期「FFミドシップ」を標榜するクルマがありましたが、いつの間にか消えてしまいました。前輪荷重が60%くらいしかなかったのでトラクションの問題もあったと推測します。

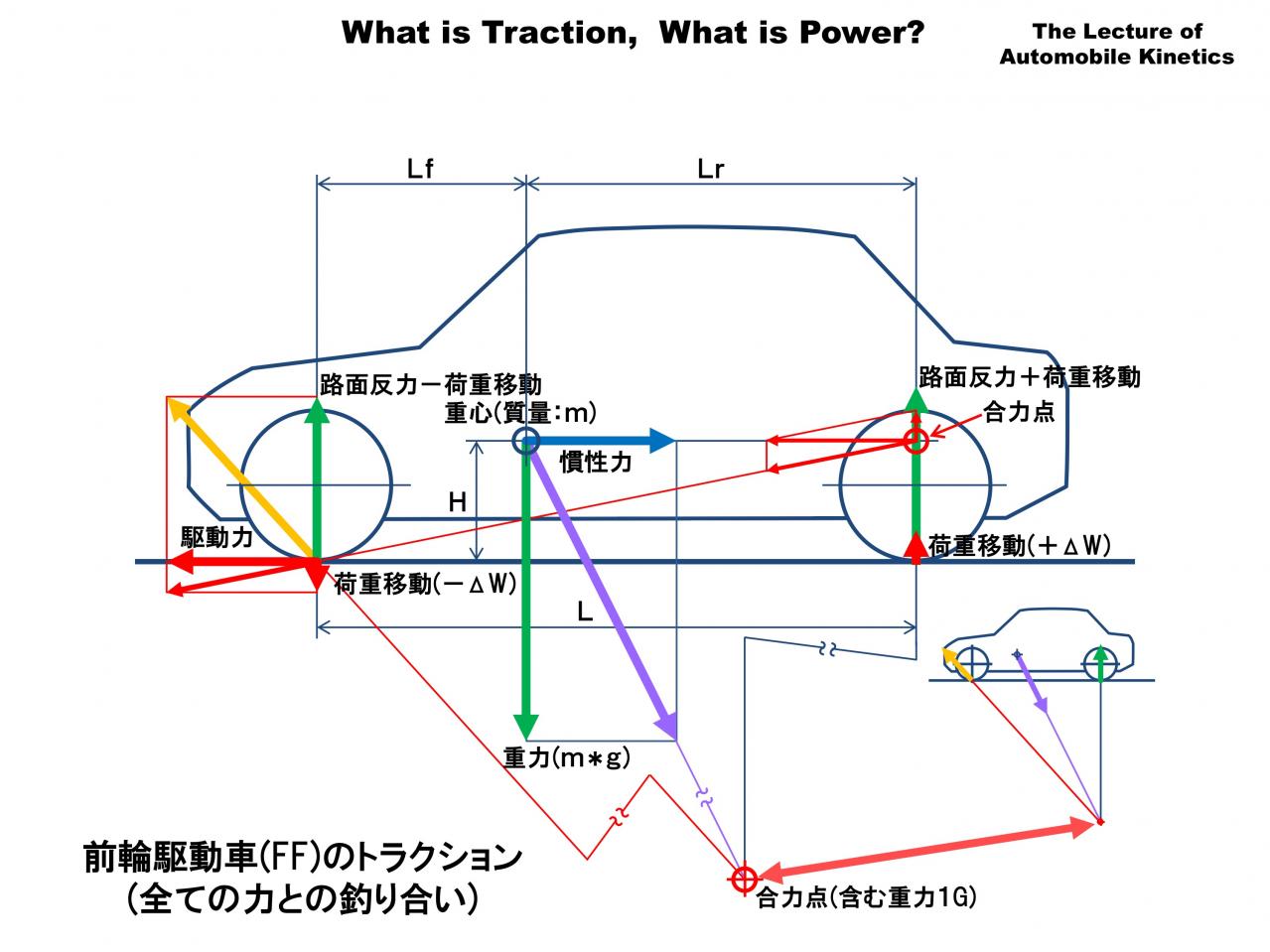
この図は重力の釣り合いと、駆動力の釣り合いを合算したものです。重力と路面反力、駆動力と慣性力をすべて合わせた力の釣り合いの合力点は後輪の真下でかなり低いところになります。

加速の限界はパワーが十分にある場合は路面とタイヤの摩擦力で加速度の上限が決まってしまいます。トラクションは元々の重心の前後位置で決まる駆動輪荷重と加速時に発生する動的な前後荷重移動、それに路面とタイヤの摩擦係数で決まります。前輪駆動車（FF）は加速すると前輪の接地荷重が減少するのでトラクション上不利になります。FFでトラクションを確保するためには重心をかなり前寄りにしておく必要があります。

FF車の前輪荷重配分がかなり大きいのはパワートレインが前部に集中しているからだけでなく、そういうレイアウトにしておかないとトラクションが確保できないからです。またFFはFRとは逆に重心高が低く、前方にあり、ホイールベースは長い方が加速時の前輪接地荷重の減少が小さくなってトラクション上は有利です。

ここまで前準備ができたところで、いよいよ「大馬力のFFがない理由（トラクション効率）」の講義に入ります。

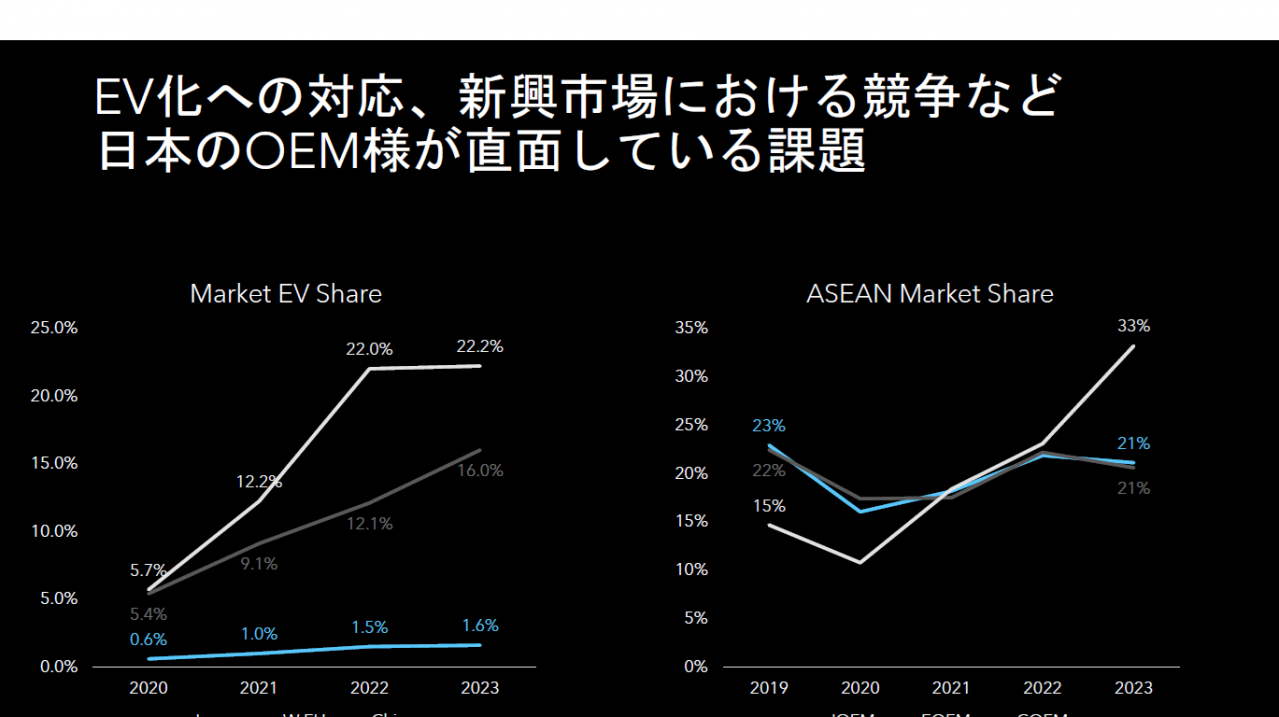
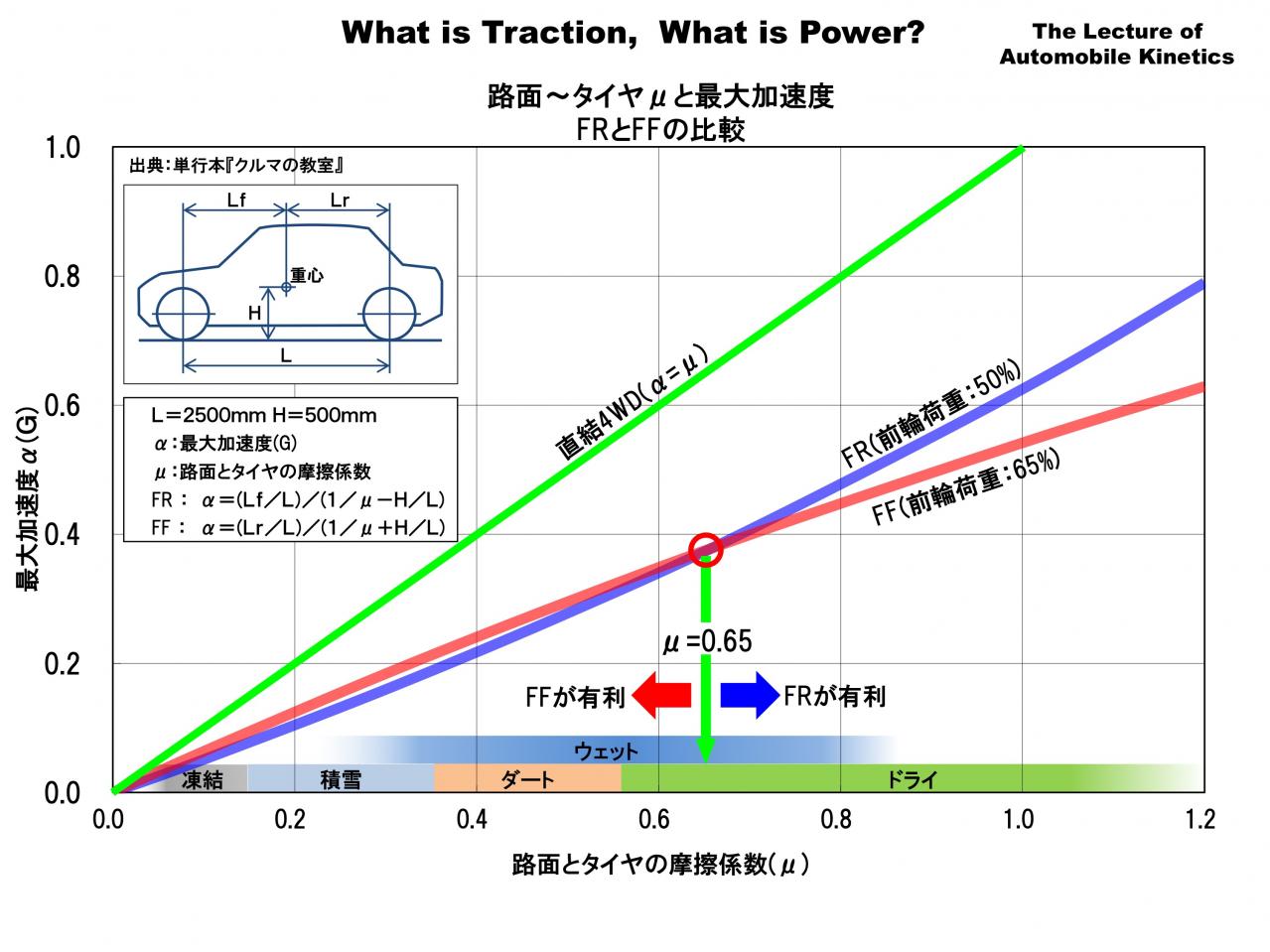
よく「FFは雪道に強い」といいますが、はたして本当なのでしょうか？　このグラフを見てみましょう。横軸が路面とタイヤの摩擦係数(μ)、縦軸が最大加速度α(G)の「μ－α線図」です。

横軸の数字をイメージするために路面状態の目安を書いています。　凍結してツルツルになった路面は摩擦係数がμ=0.1くらい、積雪した路面はμ=0.2-0.3、乾いたアスファルト路面（ドライ）ではタイヤの性能にもよりますがμ=0.6-1.2くらい、ダート（未舗装）路面やウェット（濡れた舗装路）はその間くらいです。

縦軸は、ある摩擦係数(μ)の時に、そのクルマが出せる最大の加速度を表しています。この最大加速度はいくらパワーを上げても、ギヤ比を変えても、これ以上は加速できない「トラクションの限界」です。

青線はFR車で前後輪の荷重配分が50:50、赤線はFF車で前後輪の荷重配分が65:35です。このグラフは図中の式で計算して描かれています。図中の式を言葉を交えて書くと以下のようになります。

　FR車の最大加速度(α)=後輪荷重配分(Lf/L)/(1/摩擦係数(μ)－重心高とホイールベースの比(H/L))
　FF車の最大加速度(α)=前輪荷重配分(Lr/L)/(1/摩擦係数(μ)＋重心高とホイールベースの比(H/L))
　
原点（μ=0）付近の曲線の傾きは駆動輪の荷重配分で決まります。駆動輪荷重の大きいFFの方が傾きが大きく、トラクションが大きい。そこからの曲線の変化は駆動輪への荷重移動の増減によるものです。

FRは荷重移動によって駆動輪の荷重が増加するため、摩擦係数が大きくなるほど傾きが大きく（下に凸）なります。FFは荷重移動によって駆動輪の荷重が減少するため、傾きが小さく（上に凸）になります。そのため摩擦係数(μ)がμ=0.65あたりでグラフが交差し、その点以下のところではFFが上に、それ以上のところではFRのグラフの方が上になります。

これが「FFは雪道に強い」といわれている根拠です。しかし、逆にドライ路面ではFFはFRに比べて最大加速度が低い…「FFはドライ路面に弱い」のです。

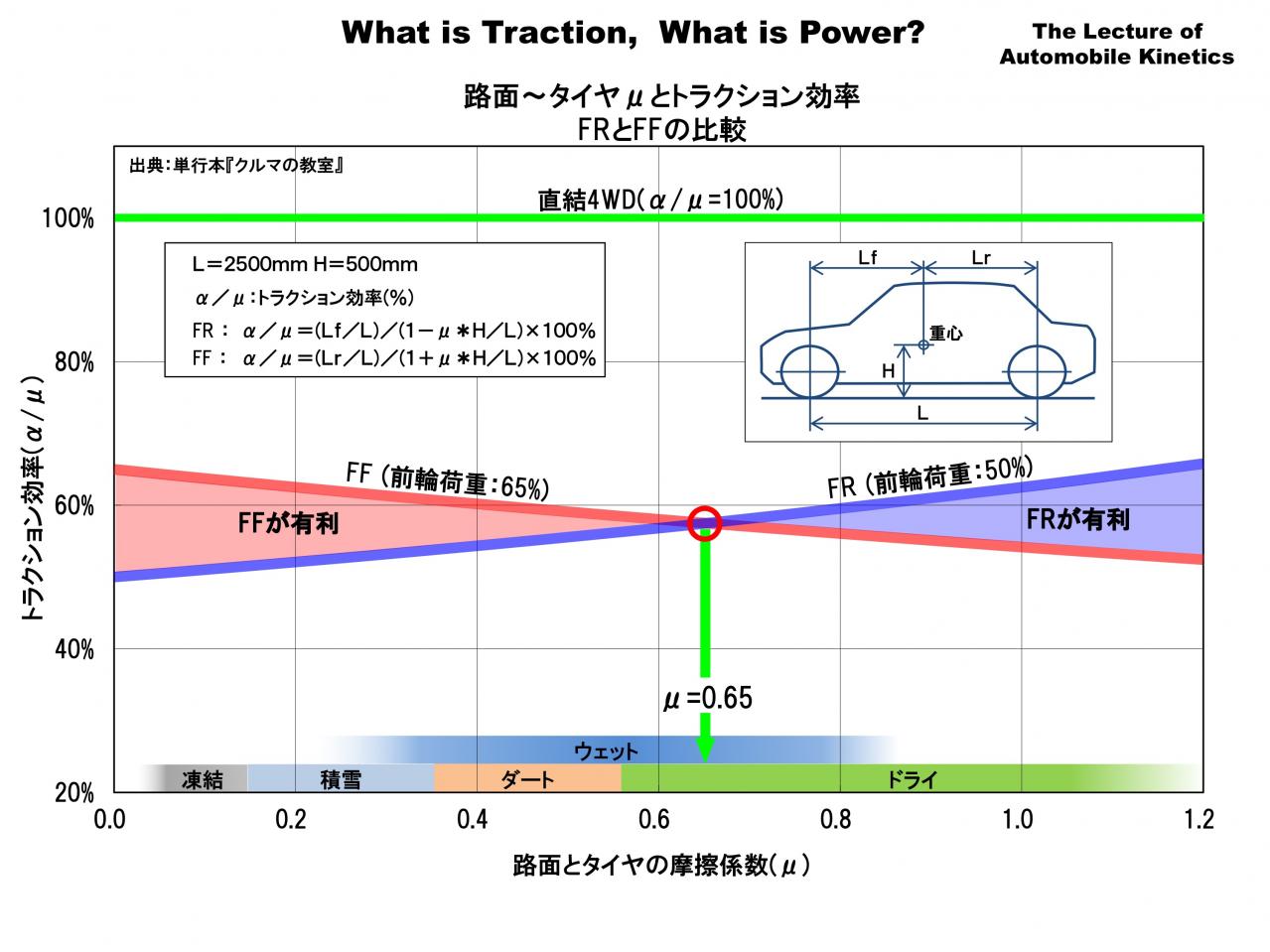
この図は前の図をわかりやすくするため、縦軸をトラクション効率（α/μ）に替えたものです。トラクション効率というのは最大加速度α(G)を路面とタイヤの摩擦係数(μ)で割ったもので、これは「路面とタイヤの摩擦をどれくらい効率的に利用できているか」という指標になります。

トラクション効率が全域で100%という代表例が直結4WDです。したがってトラクション効率は無敵の直結4WDにどれくらい迫れているか？という指標でもあります。

グラフを見ると路面とタイヤの摩擦係数が低いところではFFのトラクション効率が高く、摩擦係数が高いところではFRが高くなっています。それらが交差する点がμ=0.65です。このグラフを見ると 「雪道に強く、ドライ路面に弱いFF」のトラクション性能がよくわかります。

またFR、FFともにトラクション効率が概略50-65%近辺にあります。つまり前後どちらかのタイヤだけを駆動する一般的なFRやFFは直結4WDの6割くらいのトラクション効率しかないということです。

しかし、そのクルマがさほどパワフルではなく、発進加速が最大でも0.5Gしか出せなければ、このグラフの右半分は架空の話になります。だからハッチバックやミニバンのようなファミリーカーで、おとなしい運転をされる場合にはドライ路面ではFF車とFR車の差は感じられないでしょう。逆に積雪路や凍結路は状況によっては誰でも走らざるを得ないので、FF車の方がずっと安心です。

しかし、そのクルマが大出力のエンジンやモーター／バッテリーシステムを持っていて、乗られる方が加速を楽しみたいと思うのであれば、FF車は選ばない方が賢明です。この図の右半分が重要になるからです。

「大馬力のFFがない理由」は正にこれなのです。

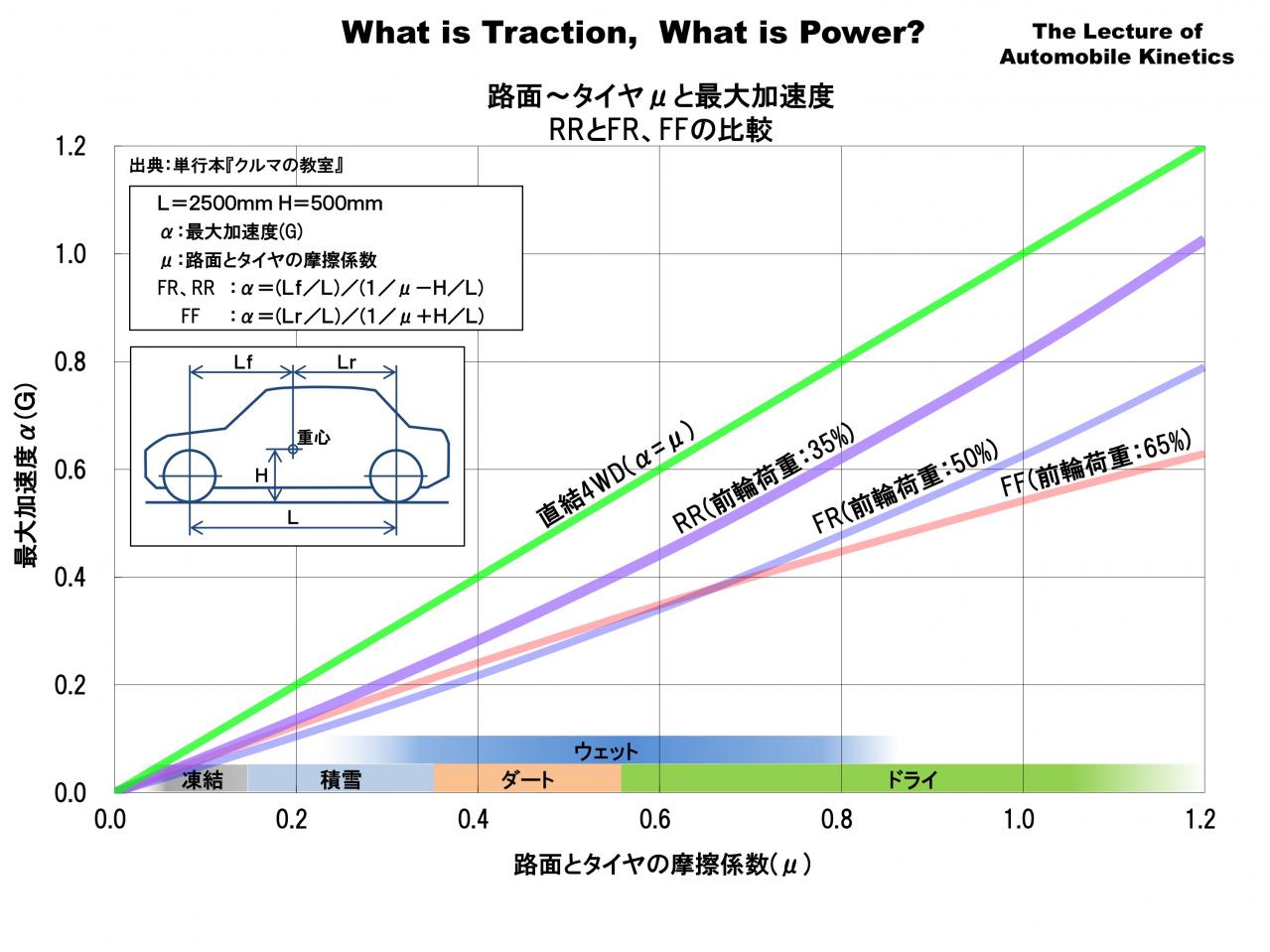
少し脱線してFRとFFの「μ－α線図」 に後輪駆動の究極であるリヤエンジン・リヤドライブ（RR）車を加えてみました。このシミュレーションでは前後荷重配分を35:65としています。

直結4WDの「μ－α線図」は路面とタイヤの摩擦係数(μ)=最大加速度(α) の直線です。トラクション効率は100%となり、これ以上はレーシングカーのような「空力的ダウンフォース」を用いない限りあり得ません。

その直結4WDに高μ領域で肉薄するのがRRです。駆動輪の荷重配分が大きいので原点（μ=0）付近でグラフの傾きが大きく、さらに後輪駆動の特性でグラフが下に凸のカーブになっているので、路面とタイヤの摩擦係数が大きくなればなるほど直結4WDに近づきます。ことトラクションに関してはRRは2輪駆動の中では最強です。

RRは高μ領域では直結4WDにかなり迫っていて、しかもグラフが下に凸になっているので摩擦係数(μ)が1.2よりさらに大きいところではどうなるのか？　もしかすると直結4WDを超えてしまうのでは？と思った方はいませんか。それでは次のグラフでそれを確かめてみましょう！

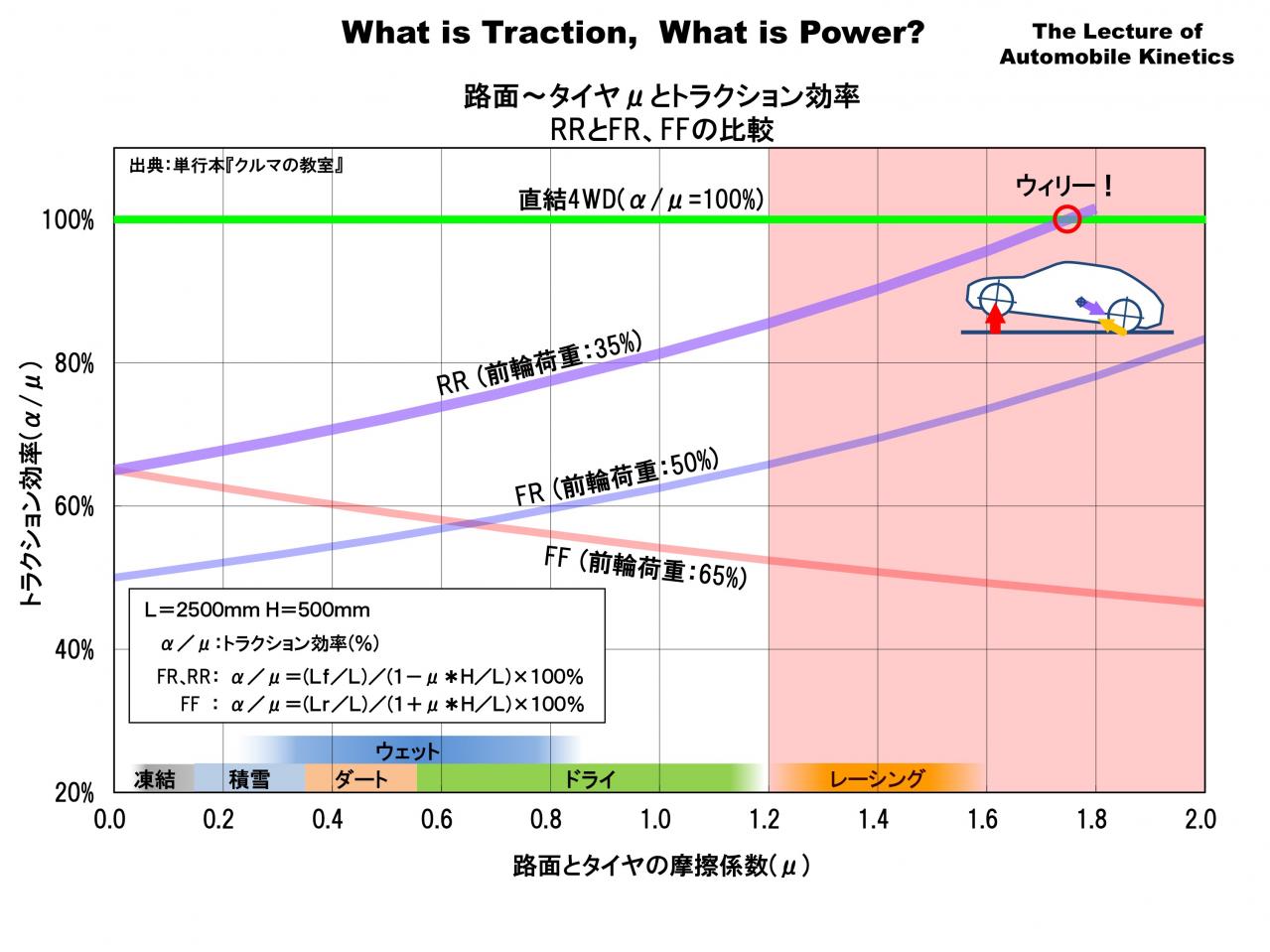
前の図と同じデータをトラクション効率(α／μ)のグラフにし、さらに横軸を通常ではありえない摩擦係数まで拡大してみました。

RRはμ=1.75あたりで直結4WDの100%を超えてしまいます。「やはり直結4WDを超えたか！」と思われたかもしれませんが、実はこの点で前輪荷重がゼロになり、ウィリー（前輪が浮き上がる）してしまい、これ以上加速できなくなります。やはりトラクション効率の物理限界は100%です。

サーキット路面とレーシングタイヤの摩擦係数はμ=1.4-1.6くらいが上限と思われますので、その状態でのRRのトラクション効率は90%以上になります。少なくともサーキットのドライ路面では無敵です。

さらにRRは制動の面でも有利です。制動時は後輪から前輪への荷重移動により接地荷重がうまい具合にバランスします。１Gで制動すると荷重移動によって動的な荷重配分が静止時の35:65から50:50程度になり前後のブレーキを絶妙にバランスできるからです。FFだとこうはいきません。静止時65:35の前後荷重配分が制動時には80:20になり、極端なフロントブレーキ配分になってしまいます。